“Rothe–Hagen identity”的意思、由来-开放百科全书

词条

Rothe–Hagen identity

释义

References

In mathematics, the Rothe–Hagen identity is a mathematical identity valid for all complex numbers (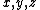) except where its denominators vanish:

It is a generalization of Vandermonde's identity, and is named after Heinrich August Rothe and Johann Georg Hagen.

References

{{citation

| last = Chu | first = Wenchang
| issue = 1
| journal = Electronic Journal of Combinatorics
| at = N24
| title = Elementary proofs for convolution identities of Abel and Hagen-Rothe
| url = http://www.combinatorics.org/ojs/index.php/eljc/article/view/v17i1n24
| volume = 17
| year = 2010}}.

{{citation

| last = Gould | first = H. W.
| journal = The American Mathematical Monthly
| jstor = 2306429
| mr = 0075170
| pages = 84–91
| title = Some generalizations of Vandermonde's convolution
| volume = 63
| year = 1956}}. See especially pp. 89–91.

{{citation

| last = Hagen | first = Johann G. | authorlink = Johann Georg Hagen
| title = Synopsis Der Hoeheren Mathematik
| at = formula 17, pp. 64–68, vol. I
| location = Berlin
| year = 1891}}. As cited by {{harvtxt|Gould|1956}}.

{{citation

| last = Ma | first = Xinrong
| doi = 10.1016/j.jcta.2010.12.012
| issue = 4
| journal = Journal of Combinatorial Theory | series = Series A
| mr = 2763069
| pages = 1475–1493
| title = Two matrix inversions associated with the Hagen-Rothe formula, their q-analogues and applications
| volume = 118
| year = 2011}}.

{{citation

| last = Rothe | first = Heinrich August
| title = Formulae De Serierum Reversione Demonstratio Universalis Signis Localibus Combinatorio-Analyticorum Vicariis Exhibita: Dissertatio Academica
| url = https://books.google.com/books/about/Formulae_De_Serierum_Reversione_Demonstr.html
| location = Leipzig
| year = 1793}}. As cited by {{harvtxt|Gould|1956}}.{{DEFAULTSORT:Rothe-Hagen identity}}{{mathapplied-stub}}

3 : Factorial and binomial topics|Mathematical identities|Complex analysis

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。