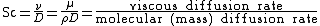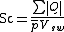请输入您要查询的百科知识：

　

词条 Schmidt number
释义

  1. Turbulent Schmidt Number

  2. Stirling engines

  3. References

  4. Notes

{{for|the measure of the quantum entanglement of a density matrix|Schmidt decomposition}}

Schmidt number (Sc) is a dimensionless number defined as the ratio of momentum diffusivity (kinematic viscosity) and mass diffusivity, and is used to characterize fluid flows in which there are simultaneous momentum and mass diffusion convection processes. It was named after the German engineer Ernst Heinrich Wilhelm Schmidt (1892–1975).

The Schmidt number is the ratio of the shear component for diffusivity viscosity/density to the diffusivity for mass transfer D. It physically relates the relative thickness of the hydrodynamic layer and mass-transfer boundary layer. Its analysis has engendered many extensions in various fields of physics.[1]

It is defined[2] as:

where:

  • is the kinematic viscosity or (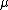/) in units of (m2/s)
  • is the mass diffusivity (m2/s).
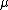  • is the dynamic viscosity of the fluid (Pa·s or N·s/m² or kg/m·s)
  • is the density of the fluid (kg/m³).

The heat transfer analog of the Schmidt number is the Prandtl number (Pr). The ratio of thermal diffusivity to mass diffusivity is the Lewis number (Le).

Turbulent Schmidt Number

The turbulent Schmidt number is commonly used in turbulence research and is defined as:[3]

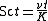
where:

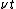  • is the eddy viscosity in units of (m2/s)
  • is the eddy diffusivity (m2/s).

The turbulent Schmidt number describes the ratio between the rates of turbulent transport of momentum and the turbulent transport of mass (or any passive scalar). It is related to the turbulent Prandtl number which is concerned with turbulent heat transfer rather than turbulent mass transfer. It is useful for solving the mass transfer problem of turbulent boundary layer flows. The simplest model for Sct is the Reynolds analogy, which yields a turbulent Schmidt number of 1. From experimental data and CFD simulations, Sct ranges from 0.4 to 3.5.

Stirling engines

For Stirling engines, the Schmidt number is related to the specific power.

Gustav Schmidt of the German Polytechnic Institute of Prague published an analysis in 1871 for the now-famous closed-form solution for an idealized isothermal Stirling engine model.[4][5]

where,

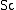  • is the Schmidt number
  • is the heat transferred into the working fluid
  • is the mean pressure of the working fluid
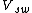  • is the volume swept by the piston.

References

1. ^{{cite journal|last1=Terhal|first1=Barbara M.|last2=Horodecki|first2=Paweł|title=Schmidt number for density matrices|journal=Physical Review A|date=6 March 2000|volume=61|issue=4|pages=040301|doi=10.1103/PhysRevA.61.040301|arxiv=quant-ph/9911117|bibcode=2000PhRvA..61d0301T}}
2. ^{{Citation | last1 = Incropera | first1 = Frank P. | last2 = DeWitt | first2 = David P. | title = Fundamentals of Heat and Mass Transfer | edition = 3rd | publisher = John Wiley & Sons | year = 1990 | pages = 345 | isbn = 978-0-471-51729-0 }} Eq. 6.71.
3. ^{{cite journal|last=Brethouwer|first=G.|title=The effect of rotation on rapidly sheared homogeneous turbulence and passive scalar transport. Linear theory and direct numerical simulation|journal=J. Fluid Mech.|year=2005|volume=542|pages=305–342|doi=10.1017/s0022112005006427|bibcode = 2005JFM...542..305B }}
4. ^Schmidt Analysis (updated 12/05/07) {{webarchive|url=https://web.archive.org/web/20080518073519/http://www.ent.ohiou.edu/~urieli/stirling/isothermal/Schmidt.html |date=2008-05-18 }}
5. ^http://mac6.ma.psu.edu/stirling/simulations/isothermal/schmidt.html

}}

Notes

{{NonDimFluMech}}

3 : Dimensionless numbers of fluid mechanics|Dimensionless numbers of thermodynamics|Fluid dynamics
随便看

　

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。

　

Copyright © 2023 OENC.NET All Rights Reserved
京ICP备2021023879号 更新时间：2024/11/13 20:45:32