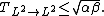- Common usage and Young's inequality
- Proof
- See also
- References
In mathematical analysis, the Schur test, named after German mathematician Issai Schur, is a bound on the  operator norm of an integral operator in terms of its Schwartz kernel (see Schwartz kernel theorem).
operator norm of an integral operator in terms of its Schwartz kernel (see Schwartz kernel theorem).
Here is one version.[1] Let  be two measurable spaces (such as
be two measurable spaces (such as  ). Let
). Let  be an integral operator with the non-negative Schwartz kernel
be an integral operator with the non-negative Schwartz kernel  ,
,  ,
, 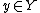 :
:
If there exist real functions  and
and  and numbers
and numbers 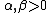 such that
such that
for almost all  and
and
for almost all  , then
, then  extends to a continuous operator
extends to a continuous operator  with the operator norm
with the operator norm
Such functions  ,
,  are called the Schur test functions.
are called the Schur test functions.
In the original version,  is a matrix and
is a matrix and  .[2]
.[2]
Common usage and Young's inequality
A common usage of the Schur test is to take 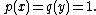 Then we get:
Then we get:
This inequality is valid no matter whether the Schwartz kernel  is non-negative or not.
is non-negative or not.
A similar statement about  operator norms is known as Young's inequality for integral operators:[3]
operator norms is known as Young's inequality for integral operators:[3]
if
where  satisfies
satisfies  , for some
, for some 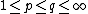 , then the operator
, then the operator  extends to a continuous operator
extends to a continuous operator  , with
, with 
Proof
Using the Cauchy–Schwarz inequality and the inequality (1), we get:
Integrating the above relation in  , using Fubini's Theorem, and applying the inequality (2), we get:
, using Fubini's Theorem, and applying the inequality (2), we get:
It follows that  for any
for any 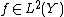 .
.
See also
- Hardy–Littlewood–Sobolev inequality
References
 spaces, Ergebnisse der Mathematik und ihrer Grenzgebiete (Results in Mathematics and Related Areas), vol. 96., Springer-Verlag, Berlin, 1978. Theorem 5.2.
spaces, Ergebnisse der Mathematik und ihrer Grenzgebiete (Results in Mathematics and Related Areas), vol. 96., Springer-Verlag, Berlin, 1978. Theorem 5.2.2. ^I. Schur, Bemerkungen zur Theorie der Beschränkten Bilinearformen mit unendlich vielen Veränderlichen, J. reine angew. Math. 140 (1911), 1–28.
3. ^Theorem 0.3.1 in: C. D. Sogge, Fourier integral operators in classical analysis, Cambridge University Press, 1993. {{ISBN|0-521-43464-5}}
- Toluidine blue
- Toluidine Blue O
- Toluidines
- Tolumnia
- Tolumnius
- To-Lun
- Tolunay Kafkas
- Tolupan
- Tolus
- Tolus appalachius
- Tolu-sol
- Toluviejo
- Toluvila statue
- Toluylene red
- Tolva
- Tolvaptan
- Tolverne
- Tolv i topp
- Tolworth Hurdle
- Tolylene diisocyanate
- Tolypangium
- Tolypeutes matacus
- Tolypeutes tricinctus
- Tolypocladium inflatum
- Tolypocladium inflatum Gams