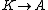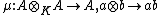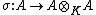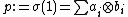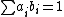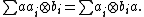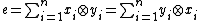“Separable algebra”的意思、由来-开放百科全书

词条

Separable algebra

释义

Definition and First Properties
Examples
Separable algebras over a field Group rings
Equivalent characterizations of separability
Relation to Frobenius algebras
Relation to formally unramified and formally étale extensions
Further results
References

In mathematics, a separable algebra is a kind of semisimple algebra. It is a generalization to associative algebras of the notion of a separable field extension.

Definition and First Properties

A ring homomorphism (of unital, but not necessarily commutative rings)

is called separable (or a separable extension) if the multiplication map

admits a splitting{{dn|date=March 2019}}

by means of a map of A-A-bimodules σ. Such a splitting σ is determined by its value

σ(1). The condition that σ splits μ then is equivalent to

and the condition to be a map of A-A-bimodules is equivalent to the following requirement for any a in A:

Such an element p is called a separability idempotent, since it satisfies .

Examples

For any commutative ring R, the (non-commutative) ring of n-by-n matrices 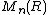is a separable R-algebra. For any 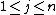, a separability idempotent is given by 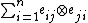, where denotes the elementary matrix which is 0 except for the entry in position (i, j), which is 1. In particular, this shows that separability idempotents need not be unique.

Separable algebras over a field

If 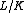is a field extension, then L is separable as an associative K-algebra if and only if the extension of fields is separable.

If L/K has a primitive element with irreducible polynomial 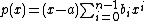, then a separability idempotent is given by 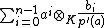. The tensorands are dual bases for the trace map: if 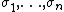are the distinct K-monomorphisms of L into an algebraic closure of K, the trace mapping Tr of L into K is defined by 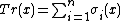. The trace map and its dual bases make explicit L as a Frobenius algebra over K.

More generally, separable algebras over a field K can be classified as follows: they are the same as finite products of matrix algebras over finite-dimensional division algebras whose centers are finite-dimensional separable field extensions of the field K. In particular: Every separable algebra is itself finite-dimensional. If K is a perfect field --- for example a field of characteristic zero, or a finite field, or an algebraically closed field --- then every extension of K is separable so that separable K-algebras are finite products of matrix algebras over finite-dimensional division algebras over field K. In other words, if K is a perfect field, there is no difference between a separable algebra over K and a finite-dimensional semisimple algebra over K.

It can be shown by a generalized theorem of Maschke that an associative K-algebra A is separable if for every field extension 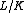the algebra 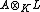is semisimple.

Group rings

If K is commutative ring and G is a finite group such that the order of G is invertible in K, then the group ring K[G] is a separable K-algebra.^[1] A separability idempotent is given by .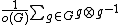

Equivalent characterizations of separability

There are a several equivalent definitions of separable algebras. A K-algebra A is separable if and only if it is projective when considered as a left module of 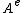in the usual way.^[2] Moreover, an algebra A is separable if and only if it is flat when considered as a right module of 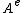in the usual way.

Separable extensions can also be characterized by means of split extensions: A is separable over K if all short exact sequences of A-A-bimodules that are split as A-K-bimodules also split as A-A-bimodules. Indeed, this condition is necessary since the multiplication mapping 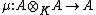arising in the definition above is a A-A-bimodule epimorphism, which is split as an A-K-bimodule map by the right inverse mapping 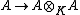given by 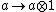. The converse can be proven by a judicious use of the separability idempotent (similarly to the proof of Maschke's theorem, applying its components within and without the splitting maps).^[3]

Equivalently, the relative Hochschild cohomology groups 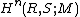of (R,S) in any coefficient bimodule M is zero for n > 0. Examples of separable extensions are many including first separable algebras where R = separable algebra and S = 1 times the ground field. Any ring R with elements a and b satisfying ab = 1, but ba different from 1, is a separable extension over the subring S generated by 1 and bRa.

Relation to Frobenius algebras

A separable algebra is said to be strongly separable if there exists a separability idempotent that is symmetric, meaning

An algebra is strongly separable if and only if its trace form is nondegenerate, thus making the algebra into a particular kind of Frobenius algebra called a symmetric algebra (not to be confused with the symmetric algebra arising as the quotient of the tensor algebra).

If K is commutative, A is a finitely generated projective separable K-module, then A is a symmetric Frobenius algebra.^[4]

Relation to formally unramified and formally étale extensions

Any separable extension A / K of commutative rings is formally unramified. The converse holds if A is a finitely generated K-algebra.^[5] A separable flat (commutative) K-algebra A is formally étale.^[6]

Further results

A theorem in the area is that of J. Cuadra that a separable Hopf-Galois extension R | S has finitely generated natural S-module R. A fundamental fact about a separable extension R | S is that it is left or right semisimple extension: a short exact sequence of left or right R-modules that is split as S-modules, is split as R-modules. In terms of G. Hochschild's relative homological algebra, one says that all R-modules are relative (R,S)-projective. Usually relative properties of subrings or ring extensions, such as the notion of separable extension, serve to promote theorems that say that the over-ring shares a property of the subring. For example, a separable extension R of a semisimple algebra S has R semisimple, which follows from the preceding discussion.

There is the celebrated Jans theorem that a finite group algebra A over a field of

characteristic p is of finite representation type if and only if its Sylow p-subgroup is cyclic: the clearest proof is to note this fact for p-groups, then note that the group algebra is a separable extension of its Sylow p-subgroup algebra B as the index is coprime to the characteristic. The separability condition above will imply every finitely generated A-module M is isomorphic to a direct summand

in its restricted, induced module. But if B has finite representation type, the restricted module

is uniquely a direct sum of multiples of finitely many indecomposables, which induce to a finite number of constituent indecomposable modules of which M is a direct sum. Hence A is of finite representation type if B is. The converse is proven by a similar argument noting that every subgroup algebra B is a B-bimodule direct summand of a group algebra A.

References

1. ^{{harvtxt|Ford|2017|loc=§4.2}}
2. ^{{harvtxt|Reiner|2003|loc=p. 102}}
3. ^{{harvtxt|Ford|2017|Theorem 4.4.1}}
4. ^{{harvtxt|Endo|Watanabe|1967|loc=Theorem 4.2}}. If A is commutative, the proof is simpler, see {{harvtxt|Kadison|1999|loc=Lemma 5.11}}
5. ^{{harvtxt|Ford|2017|loc=Corollary 4.7.2, Theorem 8.3.6}}
6. ^{{harvtxt|Ford|2017|loc=Corollary 4.7.3}}

{{cite book | last1=DeMeyer | first1=F. | last2=Ingraham | first2=E. | title=Separable algebras over commutative rings | series=Lecture Notes in Mathematics | volume=181 | location=Berlin-Heidelberg-New York | publisher=Springer-Verlag | year=1971 | isbn=978-3-540-05371-2 | zbl=0215.36602 }}
Samuel Eilenberg and Tadasi Nakayama, [https://web.archive.org/web/20110120012931/http://projecteuclid.org/DPubS?service=UI&version=1.0&verb=Display&handle=euclid.nmj%2F1118799677 On the dimension of modules and algebras. II. Frobenius algebras and quasi-Frobenius rings], Nagoya Math. J. Volume 9 (1955), 1-16.
{{Citation|author1=Endo|first1=Shizuo|author2=Watanabe|first2=Yutaka|title=On separable algebras over a commutative ring|journal=Osaka Journal of Mathematics|volume=4|year=1967|pages=233—242|mr=0227211|url=http://projecteuclid.org/euclid.ojm/1200691953}}

{{Citation|author=Ford|first=Timothy J.|title=Separable algebras|publisher=American Mathematical Society|location=Providence, RI|year=2017|isbn=978-1-4704-3770-1|mr=3618889}}
{{Citation|author=Hirata|first=H.|author2=Sugano|first2=K.|title=On semisimple and separable extensions of noncommutative rings|journal=J. Math. Soc. Japan|volume=18|year=1966|pages=360—373}}.

{{Citation|author=Kadison|first=Lars|author-link=Lars Kadison|title=New examples of Frobenius extensions|series=University Lecture Series|volume=14|publisher=American Mathematical Society|location=Providence, RI|year=1999|isbn=0-8218-1962-3|mr=1690111|doi=10.1090/ulect/014}}

{{Citation | last=Reiner | first=I. | authorlink=Irving Reiner | title=Maximal Orders | series=London Mathematical Society Monographs. New Series | volume=28 | publisher=Oxford University Press | year=2003 | isbn=0-19-852673-3 | zbl=1024.16008 }}
{{Weibel IHA}}

1 : Algebras

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。