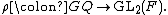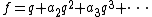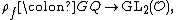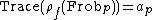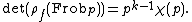- Formulation
- Optimal level and weight
- Proof
- Notes
- References
- External links
In mathematics, Serre's modularity conjecture, introduced by {{harvs|first=Jean-Pierre|last=Serre|authorlink=Jean-Pierre Serre|year1=1975|year2=1987|txt}}, states that an odd, irreducible, two-dimensional Galois representation over a finite field arises from a modular form. A stronger version of this conjecture specifies the weight and level of the modular form. The conjecture was proved by Chandrashekhar Khare in the level 1 case,[1] in 2005 and later in 2008 a proof of the full conjecture was worked out jointly by Khare and Jean-Pierre Wintenberger.[2]
Formulation
The conjecture concerns the absolute Galois group 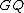 of the rational number field
of the rational number field  .
.
Let  be an absolutely irreducible, continuous, two-dimensional representation of
be an absolutely irreducible, continuous, two-dimensional representation of 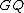 over a finite field
over a finite field 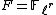 .
.
Additionally, assume  is odd, meaning the image of complex conjugation has determinant -1.
is odd, meaning the image of complex conjugation has determinant -1.
To any normalized modular eigenform
of level 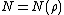 , weight
, weight 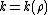 , and some Nebentype character
, and some Nebentype character
,
a theorem due to Shimura, Deligne, and Serre-Deligne attaches to  a representation
a representation
where  is the ring of integers in a finite extension of
is the ring of integers in a finite extension of 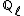 . This representation is characterized by the condition that for all prime numbers
. This representation is characterized by the condition that for all prime numbers  , coprime to
, coprime to 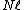 we have
we have
and
Reducing this representation modulo the maximal ideal of  gives a mod
gives a mod  representation
representation 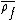 of
of 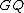 .
.
Serre's conjecture asserts that for any representation  as above, there is a modular eigenform
as above, there is a modular eigenform  such that
such that
.
The level and weight of the conjectural form  are explicitly conjectured in Serre's article. In addition, he derives a number of results from this conjecture, among them Fermat's Last Theorem and the now-proven Taniyama–Weil (or Taniyama–Shimura) conjecture, now known as the modularity theorem (although this implies Fermat's Last Theorem, Serre proves it directly from his conjecture).
are explicitly conjectured in Serre's article. In addition, he derives a number of results from this conjecture, among them Fermat's Last Theorem and the now-proven Taniyama–Weil (or Taniyama–Shimura) conjecture, now known as the modularity theorem (although this implies Fermat's Last Theorem, Serre proves it directly from his conjecture).
Optimal level and weight
The strong form of Serre's conjecture describes the level and weight of the modular form.
The optimal level is the Artin conductor of the representation, with the power of  removed.
removed.
Proof
A proof of the level 1 and small weight cases of the conjecture was obtained in 2004 by Chandrashekhar Khare and Jean-Pierre Wintenberger,[3] and by Luis Dieulefait,[4] independently.
In 2005, Chandrashekhar Khare obtained a proof of the level 1 case of Serre conjecture,[5] and in 2008 a proof of the full conjecture in collaboration with Jean-Pierre Wintenberger.[6]
Notes
2. ^{{Citation |last1=Khare |first1=Chandrashekhar |last2=Wintenberger |first2=Jean-Pierre |year=2009 |title=Serre's modularity conjecture (I) |journal=Inventiones Mathematicae |volume=178 |issue=3 |pages=485–504 |doi=10.1007/s00222-009-0205-7 |bibcode=2009InMat.178..485K |citeseerx=10.1.1.518.4611 }} and {{Citation |last1=Khare |first1=Chandrashekhar |last2=Wintenberger |first2=Jean-Pierre |year=2009 |title=Serre's modularity conjecture (II) |journal=Inventiones Mathematicae |volume=178 |issue=3 |pages=505–586 |doi=10.1007/s00222-009-0206-6 |bibcode=2009InMat.178..505K |citeseerx=10.1.1.228.8022 }}.
3. ^{{Citation |last=Khare |first=Chandrashekhar |last2=Wintenberger |first2=Jean-Pierre |year=2009 |title=On Serre's reciprocity conjecture for 2-dimensional mod p representations of Gal(Q/Q) |journal=Annals of Mathematics |volume=169 |issue=1 |pages=229–253 |doi= 10.4007/annals.2009.169.229}}.
4. ^{{Citation |last=Dieulefait |first=Luis |year=2007 |title=The level 1 weight 2 case of Serre's conjecture |journal=Revista Matemática Iberoamericana |volume=23 |issue=3 |pages=1115–1124 |url=http://projecteuclid.org/euclid.rmi/1204128312 |doi=10.4171/rmi/525|arxiv=math/0412099 }}.
5. ^{{Citation |last=Khare |first=Chandrashekhar |title=Serre's modularity conjecture: The level one case |year=2006 |journal=Duke Mathematical Journal |volume=134 |issue=3 |pages=557–589 |doi=10.1215/S0012-7094-06-13434-8 }}.
6. ^{{Citation |last=Khare |first=Chandrashekhar |last2=Wintenberger |first2=Jean-Pierre |year=2009 |title=Serre's modularity conjecture (I) |journal=Inventiones Mathematicae |volume=178 |issue=3 |pages=485–504 |doi=10.1007/s00222-009-0205-7 |bibcode=2009InMat.178..485K |citeseerx=10.1.1.518.4611 }} and {{Citation |last=Khare |first=Chandrashekhar |last2=Wintenberger |first2=Jean-Pierre |year=2009 |title=Serre's modularity conjecture (II) |journal=Inventiones Mathematicae |volume=178 |issue=3 |pages=505–586 |doi=10.1007/s00222-009-0206-6 |bibcode=2009InMat.178..505K |citeseerx=10.1.1.228.8022 }}.
References
- {{Citation | last1=Serre | first1=Jean-Pierre | author1-link=Jean-Pierre Serre | department=Journées Arithmétiques de Bordeaux (Conf., Univ. Bordeaux, 1974) |mr=0382173 | year=1975 | journal=Astérisque | issn=0303-1179 | volume=24–25 | title=Valeurs propres des opérateurs de Hecke modulo l | pages=109–117}}
- {{Citation | last1=Serre | first1=Jean-Pierre | author1-link=Jean-Pierre Serre | title=Sur les représentations modulaires de degré 2 de Gal({{overline|Q}}/Q) | doi=10.1215/S0012-7094-87-05413-5 |mr=885783 | year=1987 | journal=Duke Mathematical Journal | issn=0012-7094 | volume=54 | issue=1 | pages=179–230}}
- {{Citation | last1=Stein | first1=William A. | last2=Ribet | first2=Kenneth A. | editor1-last=Conrad | editor1-first=Brian | editor2-last=Rubin | editor2-first=Karl | title=Arithmetic algebraic geometry (Park City, UT, 1999) | publisher=American Mathematical Society | location=Providence, R.I. | series=IAS/Park City Math. Ser. | isbn=978-0-8218-2173-2 |mr=1860042 | year=2001 | volume=9 | chapter=Lectures on Serre's conjectures | pages=143–232}}
External links
- Serre's Modularity Conjecture 50 minute lecture by Ken Ribet given on October 25, 2007 ( slides PDF, [https://web.archive.org/web/20110717033621/http://www.cirm.univ-mrs.fr/videos/2007/exposes/23/Ribet.pdf other version of slides] PDF)
- [https://web.archive.org/web/20011120190728/http://modular.fas.harvard.edu/papers/serre/ribet-stein.pdf Lectures on Serre's conjectures]
- Doctor who podshock
- Doctor Who podshock
- Doctor Who: podshock
- Doctor who: Podshock
- Doctor Who ReAnimated
- Doctor Who (role-playing game)
- Doctor Who Rose
- Doctor Who RPG
- Doctor Who: Season Five
- Doctor Who: Season Four
- Doctor Who: Season One
- Doctor Who: Season Six
- Doctor Who: Season Three
- Doctor Who: Season Two
- Doctor Who serials
- Doctor who serials
- Doctor Who: Series 3 (soundtrack)
- Doctor Who Series Four
- Doctor Who Series Three
- Doctor Who ships
- Doctor Who (soundtrack)
- Doctor Who Soundtrack
- Doctor Who soundtracks
- Doctor Who spoof
- Doctor who spoofs