网巾wǎngjīn

明代成年男子用以束发的一种头巾。由落发和马尾鬃为丝编成网状，轻便透气，亦有用绢布制成者。据传明太祖微行至神乐观，见道士以茧丝结网约发，其式略似鱼网。因以颁行全国。网巾的造型类似鱼网，网口用布帛作边，俗谓“边子”。边子旁缀有金属制成的小圈，内贯绳带，绳带收束，即可约发。在网巾的上部，亦开有圆孔，并缀以绳带，使用时将发髻穿过圆孔，用绳带系拴，名曰“一统山河”；大约在明天启年间，又省去上口绳带，只束下口，名“懒收网”。《醒世姻缘传》第四十九回：“晁梁还挣挣的脱衣裳，摘网子，要上炕哩。”谢肇淛《五杂俎》卷一二：“古人帻之上加巾冠，想亦因发不齐之故。今之网巾，是其遗意……网巾以马鬃或线为之，功虽省，而巾冠不可无矣。北地苦寒，亦有以绢布为网巾者，然无屋终不可见人。”郎瑛《七修类稿》卷一四：“太祖一日微行，至神乐观。有道士于灯下结网巾。问曰：‘此何物也？’对曰：‘网巾，用以裹头，则万发俱齐。’明日，有旨召道士，命为道官，取巾十三顶颁于天下。使人无贵贱皆裹之也。”清周亮工《书影》卷九：“俗传网巾起自洪武初。新安丁南羽言，见唐人《开元八相图》，服者窄袖；有岸唐巾者，下露网纹。是古有网巾矣，或其式略异耳。”恒仁《月山诗话》：“朱竹垞云：‘余观谢宗可咏物诗有赋《网巾》云：筛影细分云缕骨，棋文斜界雪丝干。’盖元时已有之矣。”

网巾

明代男子束发用的一种网状头巾。用以裹头，使头发齐整。明初规定，士官吏民先戴网巾后着帽，但一般百姓也有单独着巾的。网巾的制作工序较复杂，式如鱼网，网口用帛作边，叫做边子。边子二帽稍后缀一小圈，用金、玉、铜、锡为之。边子的两边各系一绳，交贯于二圈之内，顶束于发。边同眉齐，加一网带，收约顶发(《蚓庵琐语》)。着时用总绳拴紧，故又名“一统山河”或名 “一统天和”。后形制上略有变化，削去网带，只束下网，改名为 “懒收网”。

网巾

网巾

由落发和马尾鬃为丝编成的似鱼网状，用以约束头发的一种头巾。因为网状，故既轻便又透气。网巾是明代首创的。据传朱元璋见神乐观的道士，用网巾裹发，便问道：“是何式？”对曰： “此网巾也，用以裹头，万 发 皆齐。” 朱元璋听后为之大悦，以为便当。因此下令照样制作，全国通行，而且规定朝服、官服的笼巾、乌纱帽下必先戴网巾。至于一般老百姓，则任其自然。因为网巾比较便利工作，故农民多是单独使用的。明代的网巾形制比现在妇女所戴的发网略复杂些。《蚓庵琐语》 中记载，网巾的形式如鱼网，网口以帛作边，叫做边子。边子二幅稍后缀一小圈，用金玉或锡为之。边子两边各系小绳交贯于二圈内，顶束于发。边与眉同齐，加一网带，收约顶发，使头发齐正。网巾除有束发作用外，还是男子成年的标志，到了一定年龄，男子才有权力戴网巾。网巾又名“一统山河”或叫做“一统天和”。天启时削去了网带，只束下网，故又名 “懒收网”。

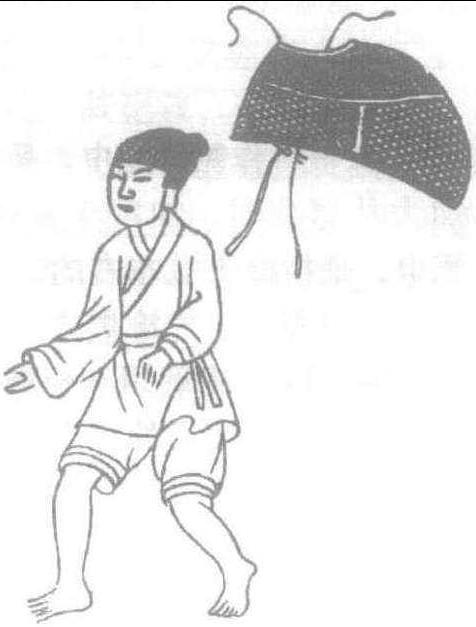
明网巾图

网巾

朝鲜族男性成年人发饰。在旧社会，朝鲜族男性成年人时兴盘结发髻，并用此巾笼发。质料用马鬃编成，状如网，前面勒于额上，后面包住后脑。