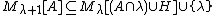1. Preliminaries

2. Silver machine

3. References

In set theory, Silver machines are devices used for bypassing the use of fine structure in proofs of statements holding in L. They were invented by set theorist Jack Silver as a means of proving global square holds in the constructible universe.

Preliminaries

An ordinal is *definable from a class of ordinals X if and only if there is a formula 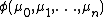and 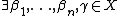such that is the unique ordinal for which where for all we define 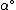to be the name for within .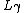

A structure 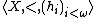is eligible if and only if:

1. .
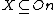2. < is the ordering on On restricted to X.
3. is a partial function from 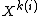to X, for some integer k(i).

If 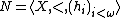is an eligible structure then 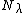is defined to be as before but with all occurrences of X replaced with .

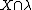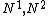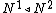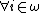Let be two eligible structures which have the same function k. Then we say if and 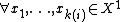we have:

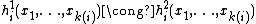
Silver machine

A Silver machine is an eligible structure of the form 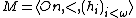which satisfies the following conditions:

Condensation principle. If 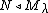then there is an such that .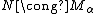

Finiteness principle. For each there is a finite set such that for any set 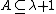we have

Skolem property. If is *definable from the set 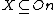, then 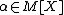; moreover there is an ordinal 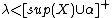, uniformly definable from 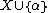, such that .

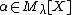References

• {{cite book | title=Constructibility | chapter=Chapter IX | author=Keith J Devlin | isbn= 0-387-13258-9 | year = 1984}}

• Mitchell Larkin
• Mitchell Lazar
• Mitchell Lee Hyman
• Mitchell Leonardo Nere
• Mitchell-Lewis Auto Company
• Mitchell-Lewis Automobile Company
• Mitchell & Lewis Company
• Mitchell-Lewis Motor Company
• Mitchell Lopez (footballer)
• Mitchell Lopez (soccer)
• Mitchell Lovelock-Fay
• Mitchell Lund
• Mitchell Mann
• Mitchell Mariners
• Mitchell Mark
• Mitchell (MCC cricketer)
• Mitchell McDeere
• Mitchell Megginson
• Mitchell Michael Grassi
• Mitchell micropolitan area
• Mitchell, Minnesota
• Mitchell Morgan
• Mitchell Moses
• Mitchell Mulhern
• Mitchell Nere