请输入您要查询的百科知识：

　

词条 Smale's problems
释义

  1. Table of problems

  2. See also

  3. References

Smale's problems are a list of eighteen unsolved problems in mathematics that was proposed by Steve Smale in 1998,[1] republished in 1999.[2] Smale composed this list in reply to a request from Vladimir Arnold, then vice-president of the International Mathematical Union, who asked several mathematicians to propose a list of problems for the 21st century. Arnold's inspiration came from the list of Hilbert's problems that had been published at the beginning of the 20th century.

Table of problems

ProblemBrief explanationStatusYear Solved
1st Riemann hypothesis: The real part of every non-trivial zero of the Riemann zeta function is 1/2. (see also Hilbert's eighth problem){{sort|3|}}Unresolved.}} –
2nd Poincaré conjecture: Every simply connected, closed 3-manifold is homeomorphic to the 3-sphere.{{sort|1|}}Resolved. Result: Yes, Proved by Grigori Perelman using Ricci flow.[3][4][5] }} 2003
3rdP versus NP problem: For all problems for which an algorithm can verify a given solution quickly (that is, in polynomial time), can an algorithm can also find that solution quickly?{{sort|3|}}Unresolved.}} –
4th Shub–Smale tau-conjecture on the integer zeros of a polynomial of one variable[6][7]– –
5th Can one decide if a Diophantine equation f(x,y) = 0 (input f ∈ 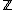[u,v]) has an integer solution, (x,y), in time (2s)c where c is a universal constant? That is, can the problem be decided in exponential time?– –
6th Is the number of relative equilibria finite, in the n-body problem of celestial mechanics, for any choice of positive real numbers m1,...,mn as the masses?{{sort|2|}}Partially resolved. Proved for five bodies by A. Albouy and V. Kaloshin in 2012.[8]}} 2012
7thdate=October 2016}} of points on the 2-sphere A noteworthy form of this problem is the Thomson Problem of equal point charges on a unit sphere governed by the electrostatic Coulomb's law. Very few exact N-point solutions are known while most solutions are numerical. Numerical solutions to this problem have been shown to correspond well with features of electron shell-filling in Atomic structure found throughout the periodic table.[9] A well-defined, intermediate step to this problem involving a point charge at the origin has been reported.[10] –
8th Extend the mathematical model of general equilibrium theory to include price adjustmentsGjerstad (2013)[11] extends the deterministic model of price adjustment to a stochastic model and shows that when the stochastic model is linearized around the equilibrium the result is the autoregressive price adjustment model used in applied econometrics. He then tests the model with price adjustment data from a general equilibrium experiment. The model performs well in a general equilibrium experiment with two commodities. –
9th The linear programming problem: Find a strongly-polynomial time algorithm which for given matrix A ∈ Rm×n and b ∈ Rm decides whether there exists x ∈ Rn with Ax ≥ b.– –
10th Pugh's closing lemma (higher order of smoothness){{sort|2|}}Partially Resolved. Proved for Hamiltonian diffeomorphisms of closed surfaces by M. Asaoka and K. Irie in 2015.[12]}} 2015
11th Is one-dimensional dynamics generally hyperbolic?T}} be approximated by one of the same degree with the property that every critical point tends to a periodic sink under iteration?") and the real-variable version ("Can a smooth map {{math|T: [0,1] → [0,1]}} be {{math|Cr}} approximated by one which is hyperbolic, for all {{math|r > 1}}?"). The former remains open even in the simplest parameter space of polynomials, the Mandelbrot set. The latter was proved by Kozlovski, Shen and van Strien[13] in 2007. –
12th Can a diffeomorphism of a compact manifold M onto itself be C approximated, all r ≥ 1, by one T : M → M which commutes with only its iterates? In other words, what are the centralizers of a diffeomorphism?{{sort|2|}}Partially Resolved. Solved in the {{math|C1}} topology by Christian Bonatti, Sylvain Crovisier and Amie Wilkinson[14] in 2009. Still open in the {{math|Cr}} topology for {{math|r > 1}}.}} 2009
13th Hilbert's 16th problem: Describe relative positions of ovals originating from a real algebraic curve and as limit cycles of a polynomial vector field on the plane.{{sort|3|}}Unresolved, even for algebraic curves of degree 8.}} –
14th Do the properties of the Lorenz attractor exhibit that of a strange attractor?{{sort|1|}}Resolved. Result: Yes, solved by Warwick Tucker using interval arithmetic.[15]}} 2002
15th Do the Navier–Stokes equations in R3 always have a unique smooth solution that extends for all time?{{sort|3|}}Unresolved.}} –
16th Jacobian conjecture: If The Jacobian determinant of F is a non-zero constant and k has characteristic 0, then F has an inverse function G: kN → kN, and G is regular (in the sense that its components are polynomials).{{sort|3|}}Unresolved.}} –
17th Solving polynomial equations in polynomial time in the average case{{sort|1|}}C. Beltrán and L. M. Pardo found a uniform probabilistic algorithm (average Las Vegas algorithm) for Smale's 17th problem[16][17] F. Cucker and P. Bürgisser made the smoothed analysis of a probabilistic algorithm à la Beltrán-Pardo, and then exhibited a deterministic algorithm running in time 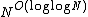.[18] Finally, P. Lairez found an alternative method to de-randomize the algorithm and thus found a deterministic algorithm which runs in average polynomial time.[19] The problem is now considered as fully solved. All these works follow Shub and Smale's foundational work (the "Bezout series") started in[20]}} –
18th Limits of intelligence (it talks about the fundamental problems of intelligence and learning, both from the human and machine side)[21]– –

In later versions, Smale also listed three additional problems, "that don’t seem important enough to merit a place on our main list, but it would still be nice to solve them:"[22][23]

  1. Mean value problem
  2. Is the three-sphere a minimal set (Gottschalk's conjecture)?
  3. Is an Anosov diffeomorphism of a compact manifold topologically the same as the Lie group model of John Franks?

See also

  • Millennium Prize Problems
  • Simon problems

References

1. ^{{cite journal | first = Steve | last = Smale|title = Mathematical Problems for the Next Century|journal = Mathematical Intelligencer|year =1998|volume=20|number=2|pages=7–15|citeseerx = 10.1.1.35.4101|doi=10.1007/bf03025291}}
2. ^{{cite book | first = Steve | last = Smale |editor1-first = V. I. | editor1-last = Arnold | editor2-first = M. | editor2-last = Atiyah | editor3-first = P. | editor3-last = Lax | editor4-first = B. | editor4-last = Mazur | title=Mathematics: frontiers and perspectives |publisher=American Mathematical Society|year=1999|pages=271–294 |chapter=Mathematical problems for the next century|isbn=978-0821820704}}
3. ^{{cite arXiv | last = Perelman | first = Grigori | authorlink = Grigori Perelman | title = The entropy formula for the Ricci flow and its geometric applications | eprint = math.DG/0211159 | year = 2002 }}
4. ^{{cite arXiv | last = Perelman | first = Grigori | title = Ricci flow with surgery on three-manifolds | eprint = math.DG/0303109 | year = 2003 }}
5. ^{{cite arXiv | last = Perelman | first = Grigori | title = Finite extinction time for the solutions to the Ricci flow on certain three-manifolds | eprint = math.DG/0307245 | year = 2003 }}
6. ^{{cite journal | last1=Shub | first1=Michael | last2=Smale | first2=Steve | title=On the intractability of Hilbert's Nullstellensatz and an algebraic version of "NP≠P?" | zbl=0882.03040 | journal=Duke Math. J. | volume=81 | pages=47–54 | year=1995 | doi=10.1215/S0012-7094-95-08105-8 }}
7. ^{{cite book | last1=Bürgisser | first1=Peter | title=Completeness and reduction in algebraic complexity theory | zbl=0948.68082 | series=Algorithms and Computation in Mathematics | volume=7 | location=Berlin | publisher=Springer-Verlag | year=2000 | isbn=978-3-540-66752-0 | page=141 }}
8. ^{{cite journal | first1 = A. | last1 = Albouy | first2 = V. | last2 = Kaloshin |title= Finiteness of central configurations of five bodies in the plane |journal=Annals of Mathematics |volume= 176 |year=2012 |pages=535–588 |doi=10.4007/annals.2012.176.1.10}}
9. ^{{cite journal|first=T., Jr|last=LaFave|title=Correspondences between the classical electrostatic Thomson Problem and atomic electronic structure|url=http://www.pagesofmind.com/FullTextPubs/La13-LaFave-2013-Correspondences-between-the-Thomson-Problem-and-Atomic-Structure.pdf|archive-url=https://web.archive.org/web/20140222100807/http://www.pagesofmind.com/FullTextPubs/La13-LaFave-2013-Correspondences-between-the-Thomson-Problem-and-Atomic-Structure.pdf|dead-url=yes|archive-date=22 February 2014|accessdate=11 Feb 2014|journal=Journal of Electrostatics|volume=71|issue=6|year=2013|pages=1029–1035|doi=10.1016/j.elstat.2013.10.001|arxiv=1403.2591}}
10. ^{{cite journal |first = T., Jr | last = LaFave |title= Discrete transformations in the Thomson Problem |url=http://www.pagesofmind.com/FullTextPubs/La14-LaFave-2014-Discrete-Transformations-in-the-Thomson-Problem.pdf|accessdate= 11 Feb 2014| journal=Journal of Electrostatics |volume= 72 |issue=1 |year=2014 |pages=39–43|doi=10.1016/j.elstat.2013.11.007|arxiv=1403.2592}}
11. ^{{cite journal | first = Steven | last = Gjerstad |title= Price Dynamics in an Exchange Economy | journal=Economic Theory |volume= 52 |issue=2 |year=2013 |pages=461–500|doi=10.1007/s00199-011-0651-5| citeseerx = 10.1.1.415.3888 }}
12. ^{{cite journal | first1 = M. | last1 = Asaoka | first2 = K. | last2 = Irie |title= A {{math|C∞}} closing lemma for Hamiltonian diffeomorphisms of closed surfaces |journal=Geometric and Functional Analysis |volume= 26 | issue = 5 |year=2016 |pages=1245–1254 |doi=10.1007/s00039-016-0386-3 }}
13. ^{{cite journal | first1 = O. | last1 = Kozlovski | first2 = W. | last2 = Shen | first3 = S. | last3 = van Strien |title= Density of hyperbolicity in dimension one|journal=Annals of Mathematics |volume= 166 |year=2007 |pages=145–182 |doi=10.4007/annals.2007.166.145}}
14. ^{{cite journal | first1 = C. | last1 = Bonatti | first2 = S. | last2 = Crovisier | first3 = A. | last3 = Wilkinson |title= The C1-generic diffeomorphism has trivial centralizer |journal=Publications Mathématiques de l'IHÉS |volume= 109 |year=2009 |pages=185–244 |doi=10.1007/s10240-009-0021-z|arxiv=0804.1416 }}
15. ^{{cite journal | first = Warwick | last = Tucker |title=A Rigorous ODE Solver and Smale's 14th Problem |journal=Foundations of Computational Mathematics |volume=2 |issue=1 |year=2002 |pages=53–117 |doi=10.1007/s002080010018 |url=http://www.math.cornell.edu/~warwick/main/rodes/JFoCM.pdf| citeseerx = 10.1.1.545.3996 }}
16. ^{{cite journal | first1 = Carlos | last1 = Beltrán | first2 = Luis Miguel | last2 = Pardo |title= On Smale's 17th Problem: A Probabilistic Positive answer |journal=Foundations of Computational Mathematics |volume=8 |issue=1 |year=2008 |pages=1–43 |doi=10.1007/s10208-005-0211-0 |url=http://personales.unican.es/beltranc/archivos/Smale17FoCM.pdf| citeseerx = 10.1.1.211.3321 }}
17. ^{{cite journal | first1 = Carlos | last1 = Beltrán | first2 = Luis Miguel | last2 = Pardo |title= Smale's 17th Problem: Average Polynomial Time to compute affine and projective solutions|journal=Journal of the American Mathematical Society|volume=22 | issue = 2 |year=2009 |pages=363–385|url=http://personales.unican.es/beltranc/archivos/AffSmale17JAMS.pdf |doi=10.1090/s0894-0347-08-00630-9|bibcode=2009JAMS...22..363B}}
18. ^{{cite journal | first1 = Felipe | last1 = Cucker | first2 = Peter | last2 = Bürgisser |title= On a problem posed by Steve Smale|journal=Annals of Mathematics |volume=174 |issue=3|year=2011 |doi=10.4007/annals.2011.174.3.8 |pages=1785–1836}}
19. ^{{cite journal | first1 = Pierre | last1 = Lairez |title= A deterministic algorithm to compute approximate roots of polynomial systems in polynomial average time |journal=Foundations of Computational Mathematics |volume=to appear |year=2016 }}
20. ^{{cite journal | first1 = Michael | last1 = Shub | first2 = Stephen | last2 = Smale |title= Complexity of Bézout's theorem. I. Geometric aspects |journal=J. Amer. Math. Soc. |volume=6 |issue=2 |year=1993 |pages=459–501 |doi=10.2307/2152805| jstor = 2152805 }}.
21. ^{{cite web |url=http://recursed.blogspot.jp/2006/02/tucson-day-3-interview-with-steve.html |date=February 3, 2006 |title=Tucson - Day 3 - Interview with Steve Smale |website=Recursivity}}
22. ^{{Cite web|url=http://www6.cityu.edu.hk/ma/doc/people/smales/pap104.pdf|title=Mathematical Problems for the Next Century|last=Smale|first=Steve|date=|website=|access-date=}}
23. ^{{Cite journal|last=Smale|first=Steve|date=|title=Mathematical problems for the next century, Mathematics: Frontiers and perspectives|url=|journal=American Mathematical Society, Providence, RI|volume=|pages=271–294|via=}}

1 : Unsolved problems in mathematics
随便看

　

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。

　

Copyright © 2023 OENC.NET All Rights Reserved
京ICP备2021023879号 更新时间：2024/11/14 15:03:21