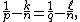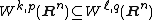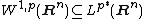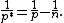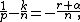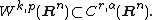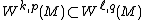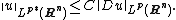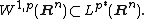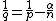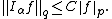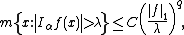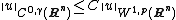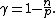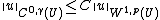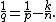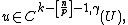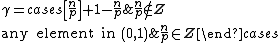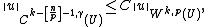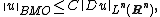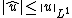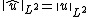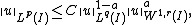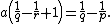“Sobolev inequality”的意思、由来-开放百科全书

词条

Sobolev inequality

释义

Sobolev embedding theorem
Generalizations Kondrachov embedding theorem
Gagliardo–Nirenberg–Sobolev inequality
Hardy–Littlewood–Sobolev lemma
Morrey's inequality
General Sobolev inequalities
{{math|k < n/p}} {{math|k > n/p}}
Case
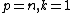
Nash inequality
References

In mathematics, there is in mathematical analysis a class of Sobolev inequalities, relating norms including those of Sobolev spaces. These are used to prove the Sobolev embedding theorem, giving inclusions between certain Sobolev spaces, and the Rellich–Kondrachov theorem showing that under slightly stronger conditions some Sobolev spaces are compactly embedded in others. They are named after Sergei Lvovich Sobolev.

Sobolev embedding theorem

Let {{math|W^k,p(Rⁿ)}} denote the Sobolev space consisting of all real-valued functions on {{math|Rⁿ}} whose first {{mvar|k}} weak derivatives are functions in {{math|L^p}}. Here {{mvar|k}} is a non-negative integer and {{math|1 ≤ p < ∞}}. The first part of the Sobolev embedding theorem states that if {{math|k > ℓ}} and {{math|1 ≤ p < q < ∞}} are two real numbers such that {{math|(k − ℓ)p < n}} and:

then

and the embedding is continuous. In the special case of {{math|k {{=}} 1}} and {{math|ℓ {{=}} 0}}, Sobolev embedding gives

where {{math|p^∗}} is the Sobolev conjugate of {{mvar|p}}, given by

This special case of the Sobolev embedding is a direct consequence of the Gagliardo–Nirenberg–Sobolev inequality.

The second part of the Sobolev embedding theorem applies to embeddings in Hölder spaces {{math|C^r,α(Rⁿ)}}. If {{math|n < p}} and

with {{math|α ∈ (0, 1]}} then one has the embedding

This part of the Sobolev embedding is a direct consequence of Morrey's inequality. Intuitively, this inclusion expresses the fact that the existence of sufficiently many weak derivatives implies some continuity of the classical derivatives.

Generalizations

The Sobolev embedding theorem holds for Sobolev spaces {{math|W^k,p(M)}} on other suitable domains {{mvar|M}}. In particular ({{harvnb|Aubin|1982|loc=Chapter 2}}; {{harvnb|Aubin|1976}}), both parts of the Sobolev embedding hold when

{{mvar|M}} is a bounded open set in {{math|Rⁿ}} with Lipschitz boundary (or whose boundary satisfies the cone condition; {{harvnb|Adams|1975|loc=Theorem 5.4}})
{{mvar|M}} is a compact Riemannian manifold
{{mvar|M}} is a compact Riemannian manifold with boundary with Lipschitz boundary
{{mvar|M}} is a complete Riemannian manifold with injectivity radius {{math|δ > 0}} and bounded sectional curvature.

Kondrachov embedding theorem

On a compact manifold with {{math|C¹}} boundary, the Kondrachov embedding theorem states that if {{math|k > ℓ}} and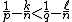then the Sobolev embedding

is completely continuous (compact). Note that the condition is just as in the first part of the Sobolev embedding theorem, with the equality replaced by an inequality, thus requiring a more regular space {{math|W^k,p(M)}}.

Gagliardo–Nirenberg–Sobolev inequality

Assume that {{mvar|u}} is a continuously differentiable real-valued function on {{math|Rⁿ}} with compact support. Then for {{math|1 ≤ p < n}} there is a constant {{mvar|C}} depending only on {{mvar|n}} and {{mvar|p}} such that

with 1/p* = 1/p - 1/n.

The case 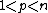is due to Sobolev, 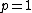to Gagliardo and Nirenberg independently. The Gagliardo–Nirenberg–Sobolev inequality implies directly the Sobolev embedding

The embeddings in other orders on {{math|Rⁿ}} are then obtained by suitable iteration.

Hardy–Littlewood–Sobolev lemma

Sobolev's original proof of the Sobolev embedding theorem relied on the following, sometimes known as the Hardy–Littlewood–Sobolev fractional integration theorem. An equivalent statement is known as the Sobolev lemma in {{harv|Aubin|1982|loc=Chapter 2}}. A proof is in {{harv|Stein|loc=Chapter V, §1.3}}.

Let {{math|0 < α < n}} and {{math|1 < p < q < ∞}}. Let {{math|I_α {{=}} (−Δ)^−α/2}} be the Riesz potential on {{math|Rⁿ}}. Then, for {{mvar|q}} defined by

there exists a constant {{mvar|C}} depending only on {{mvar|p}} such that

If {{math|p {{=}} 1}}, then one has two possible replacement estimates. The first is the more classical weak-type estimate:

where {{math|1/q {{=}} 1 − α/n}}. Alternatively one has the estimat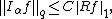ewhere 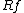is the vector-valued Riesz transform, c.f. {{harv|Schikorra | Spector | Van Schaftingen}}. The boundedness of the Riesz transforms implies that the latter inequality gives a unified way to write the family of inequalities for the Riesz potential.

The Hardy–Littlewood–Sobolev lemma implies the Sobolev embedding essentially by the relationship between the Riesz transforms and the Riesz potentials.

Morrey's inequality

Assume {{math|n < p ≤ ∞}}. Then there exists a constant {{mvar|C}}, depending only on {{mvar|p}} and {{mvar|n}}, such that

for all {{math|u ∈ C¹(Rⁿ) ∩ L^p(Rⁿ)}}, where

Thus if {{math|u ∈ W^1,p(Rⁿ)}}, then {{mvar|u}} is in fact Hölder continuous of exponent {{mvar|γ}}, after possibly being redefined on a set of measure 0.

A similar result holds in a bounded domain {{mvar|U}} with {{math|C¹}} boundary. In this case,

where the constant {{mvar|C}} depends now on {{math|n, p}} and {{mvar|U}}. This version of the inequality follows from the previous one by applying the norm-preserving extension of {{math|W^1,p(U)}} to {{math|W^1,p(Rⁿ)}}.

General Sobolev inequalities

Let {{mvar|U}} be a bounded open subset of {{math|Rⁿ}}, with a {{math|C¹}} boundary. ({{mvar|U}} may also be unbounded, but in this case its boundary, if it exists, must be sufficiently well-behaved.) Assume {{math|u ∈ W^k,p(U)}}, then we consider two cases:

In this case {{math|u ∈ L^q(U)}}, where

We have in addition the estimate

,

the constant {{mvar|C}} depending only on {{math|k, p, n}}, and {{mvar|U}}.

Here, {{mvar|u}} belongs to a Hölder space, more precisely:

where

We have in addition the estimate

the constant {{mvar|C}} depending only on {{math|k, p, n, γ}}, and {{mvar|U}}.

Case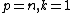

If 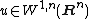, then {{mvar|u}} is a function of bounded mean oscillation and

for some constant {{mvar|C}} depending only on {{mvar|n}}. This estimate is a corollary of the Poincaré inequality.

Nash inequality

The Nash inequality, introduced by {{harvs|first=John|last=Nash|authorlink=John Forbes Nash, Jr.|year=1958|txt}}, states that there exists a constant {{math|C > 0}}, such that for all {{math|u ∈ L¹(Rⁿ) ∩ W^1,2(Rⁿ)}},

The inequality follows from basic properties of the Fourier transform. Indeed, integrating over the complement of the ball of radius {{mvar|ρ}},

{{NumBlk|:|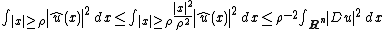

|{{EquationRef|1}}}}

by Parseval's theorem. On the other hand, one has

which, when integrated over the ball of radius {{mvar|ρ}} gives

{{NumBlk|:|

|{{EquationRef|2}}}}

where {{math|ω_n}} is the volume of the {{mvar|n}}-ball. Choosing {{mvar|ρ}} to minimize the sum of ({{EquationNote|1}}) and ({{EquationNote|2}}) and again applying Parseval's theorem:

gives the inequality.

In the special case of {{math|n {{=}} 1}}, the Nash inequality can be extended to the {{math|L^p}} case, in which case it is a generalization of the Gagliardo-Nirenberg-Sobolev inequality ({{harvnb|Brezis|2011}}, Comments on Chapter 8). In fact, if {{mvar|I}} is a bounded interval, then for all {{math|1 ≤ r < ∞}} and all {{math|1 ≤ q ≤ p < ∞}} the following inequality holds

where:

References

{{citation|mr=0450957|last= Adams|first= Robert A.|title=Sobolev Spaces|series=Pure and Applied Mathematics |volume=65|publisher= Academic Press | year= 1975| isbn=978-0-12-044150-1 }}.
{{Citation|last1=Aubin| first1=Thierry | title=Espaces de Sobolev sur les variétés riemanniennes | mr=0488125 | year=1976 | journal=Bulletin des Sciences Mathématiques |series=2e Série | volume=100 | issue=2 | pages=149–173}}
{{Citation|last1=Aubin| first1=Thierry | title=Nonlinear analysis on manifolds. Monge-Ampère equations | publisher=Springer-Verlag | series=Grundlehren der Mathematischen Wissenschaften [Fundamental Principles of Mathematical Sciences] | isbn=978-0-387-90704-8 | mr=681859 | year=1982 | volume=252 | doi=10.1007/978-1-4612-5734-9}}.
{{citation|first=Haïm|last=Brezis|authorlink=Haïm Brezis|title=Analyse Fonctionnelle: théorie et applications|publisher=Masson|location=Paris|year=1983|isbn=0-8218-0772-2}}
{{citation|first=Haïm|last=Brezis|authorlink=Haïm Brezis|title=Functional Analysis, Sobolev Spaces and Partial Differential Equations|publisher=Springer Science & Business Media|year=2011|ISBN=978-0-387-70913-0}}
{{citation|first=Lawrence|last=Evans|authorlink=Lawrence C. Evans| title=Partial Differential Equations | publisher= American Mathematical Society |location=Providence RI | year=1998 | isbn=0-8218-0772-2}}
{{citation| last= Leoni | first= Giovanni | year= 2009 | url= http://bookstore.ams.org/gsm-105 | title= A First Course in Sobolev Spaces | series= Graduate Studies in Mathematics | publisher= American Mathematical Society| isbn= 978-0-8218-4768-8}} {{MR|2527916}}, {{Zbl|1180.46001}}, MAA review
{{citation|last=Maz'ja|first=Vladimir G.|authorlink= Vladimir Maz'ja|title=Sobolev Spaces|series=Springer Series in Soviet Mathematics|publisher=Springer-Verlag|year=1985}}, Translated from the Russian by T. O. Shaposhnikova.
{{citation|last=Nash|first=J.|authorlink=John Forbes Nash, Jr.|title=Continuity of solutions of parabolic and elliptic equations|journal= American Journal of Mathematics |volume=80|year=1958|pages=931–954| doi=10.2307/2372841 |jstor=2372841| issue=4}}.
{{springer|id=i/i050230|title=Imbedding theorems|first=S.M.|last= Nikol'skii}}
{{Citation| title=An -type estimate for Riesz potentials|last1=Schikorra|last2=Spector|last3= Van Schaftingen| first1=Armin | first2=Daniel | first3=Jean |journal= Revista Matemática Iberoamericana |volume=33 |year=2017 |issue=1 |pages=291-304|arxiv=1411.2318 | doi=10.4171/rmi/937}}
{{citation|first=Elias|last=Stein|authorlink=Elias Stein|title=Singular Integrals and Differentiability Properties of Functions|publisher=Princeton University Press|location=Princeton, NJ|year=1970|isbn=0-691-08079-8}}

3 : Inequalities|Sobolev spaces|Compactness theorems

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。