“Span (category theory)”的意思、由来-开放百科全书

词条

Span (category theory)

释义

Formal definition
Examples
Cospans
See also
References

In category theory, a span, roof or correspondence is a generalization of the notion of relation between two objects of a category. When the category has all pullbacks (and satisfies a small number of other conditions), spans can be considered as morphisms in a category of fractions.

Formal definition

A span is a diagram of type 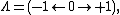i.e., a diagram of the form .

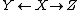That is, let Λ be the category (-1 ← 0 → +1). Then a span in a category C is a functor S:Λ → C. This means that a span consists of three objects X, Y and Z of C and morphisms f:X → Y and g:X → Z: it is two maps with common domain.

The colimit of a span is a pushout.

Examples

If R is a relation between sets X and Y (i.e. a subset of X × Y), then X ← R → Y is a span, where the maps are the projection maps 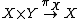and .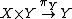
Any object yields the trivial span 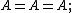formally, the diagram A ← A → A, where the maps are the identity.
More generally, let 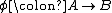be a morphism in some category. There is a trivial span A = A → B; formally, the diagram A ← A → B, where the left map is the identity on A, and the right map is the given map φ.
If M is a model category, with W the set of weak equivalences, then the spans of the form 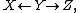where the left morphism is in W, can be considered a generalised morphism (i.e., where one "inverts the weak equivalences"). Note that this is not the usual point of view taken when dealing with model categories.

Cospans

A cospan K in a category C is a functor K:Λ^op → C; equivalently, a contravariant functor from Λ to C. That is, a diagram of type 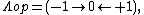i.e., a diagram of the form .

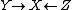Thus it consists of three objects X, Y and Z of C and morphisms f:Y → X and g:Z → X: it is two maps with common codomain.

The limit of a cospan is a pullback.

An example of a cospan is a cobordism W between two manifolds M and N, where the two maps are the inclusions into W. Note that while cobordisms are cospans, the category of cobordisms is not a "cospan category": it is not the category of all cospans in "the category of manifolds with inclusions on the boundary", but rather a subcategory thereof, as the requirement that M and N form a partition of the boundary of W is a global constraint.

The category nCob of finite-dimensional cobordisms is a dagger compact category. More generally, the category Span(C) of spans on any category C with finite limits is also dagger compact.

References

{{nlab|id=span}}

1 : Functors

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。

Formal definition

Examples

Cospans

See also

References