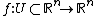- Stable manifold theorem
- See also
- Notes
- References
- External links
In mathematics, especially in the study of dynamical systems and differential equations, the stable manifold theorem is an important result about the structure of the set of orbits approaching a given hyperbolic fixed point.
Stable manifold theorem
Let
be a smooth map with hyperbolic fixed point at 
. We denote by 
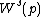the stable set and by 
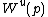the unstable set of .
The theorem[1][2][3] states that
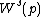- is a smooth manifold and its tangent space has the same dimension as the stable space of the linearization of
at . - 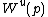is a smooth manifold and its tangent space has the same dimension as the unstable space of the linearization of at .
Accordingly 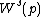is a stable manifold and 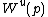is an unstable manifold.
See also
- Center manifold theorem
- Lyapunov exponent
Notes
References
- {{cite book |first=Lawrence |last=Perko |title=Differential Equations and Dynamical Systems |location=New York |publisher=Springer |edition=Third |year=2001 |isbn=0-387-95116-4 |pages=105–117 }}
- {{cite book |first=S. S. |last=Sritharan |title=Invariant Manifold Theory for Hydrodynamic Transition |location= |publisher=John Wiley & Sons |year=1990 |isbn=0-582-06781-2 }}
External links
- {{PlanetMath|title=StableManifoldTheorem|urlname=StableManifoldTheorem}}
2 : Dynamical systems|Theorems in dynamical systems