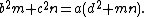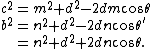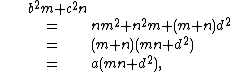“Stewart's theorem”的意思、由来-开放百科全书

词条

Stewart's theorem

释义

Statement
Proof
History
See also
Notes
References
Further reading
External links

In geometry, Stewart's theorem yields a relation between the lengths of the sides and the length of a cevian in a triangle. Its name is in honor of the Scottish mathematician Matthew Stewart, who published the theorem in 1746.^[1]

Statement

Let , , and be the lengths of the sides of a triangle. Let be the length of a cevian to the side of length . If the cevian divides the side of length into two segments of length and , with adjacent to and adjacent to , then Stewart's theorem states that

The theorem may be written more symmetrically using signed lengths of segments. That is, take the length AB to be positive or negative according to whether A is to the left or right of B in some fixed orientation of the line. In this formulation, the theorem states that if A, B, and C are colinear points, and P is any point, then

^[2]

In the special case that the cevian is the median (that is, it divides the opposite side into two segments of equal length), the result is known as Apollonius' theorem.

A common mnemonic used by students to memorize the theorem is: A man and his dad put a bomb in the sink (man+dad=bmb+cnc)

Proof

The theorem can be proved as an application of the law of cosines.^[3]{{better source|date=March 2018}}

Let θ be the angle between m and d and θ′ the angle between n and d. Then θ′ is the supplement of θ, and so and {{math|cos θ′ {{=}} −cos θ}}. Applying the law of cosines in the two small triangles using angles θ and θ′ produces

Multiplying the first equation by n and the second equation by m and adding them eliminates {{math|cos θ}}. One obtains

which is the required equation.

Alternatively, the theorem can be proved by drawing a perpendicular from the vertex of the triangle to the base and using the Pythagorean theorem to write the distances b, c, and d in terms of the altitude. The left and right hand sides of the equation then reduce algebraically to the same expression.^[2]

History

According to {{harvtxt|Hutton|Gregory|1843|loc=p. 220}}, Stewart published the result in 1746 when he was a candidate to replace Colin Maclaurin as Professor of Mathematics at the University of Edinburgh. {{harvtxt|Coxeter|Greitzer|1967|loc=p. 6}} state that the result was probably known to Archimedes around 300 B.C.E. They go on to say (mistakenly) that the first known proof was provided by R. Simson in 1751. {{harvtxt|Hutton|Gregory|1843}} state that the result is used by Simson in 1748 and by Simpson in 1752, and its first appearance in Europe given by Lazare Carnot in 1803.

Notes

1. ^{{citation|first=Matthew|last=Stewart|title=Some General Theorems of Considerable Use in the Higher Parts of Mathematics|year=1746|publisher=Sands, Murray and Cochran|place=Edinburgh}} "Proposition II"
2. ^¹{{harvnb|Russell|1905|loc=p. 3}}
3. ^{{PlanetMath|title=Proof of Stewart's Theorem|urlname=ProofOfStewartsTheorem}}

References

{{citation|first1=H.S.M.|last1=Coxeter|first2=S.L.|last2=Greitzer|title=Geometry Revisited|year=1967|publisher=The Mathematical Association of America|series=New Mathematical Library #19|isbn=0-88385-619-0}}
{{citation |title=A Course of Mathematics|first1=C.|last1=Hutton|first2=O.|last2=Gregory |publisher=Longman, Orme & Co.|year=1843|volume=II|url=https://books.google.com/books?id=9-4GAAAAYAAJ&pg=PA219#v=onepage}}
{{citation |title=Pure Geometry

|first=John Wellesley|last=Russell|publisher=Clarendon Press|year=1905
|chapter=Chapter 1 §3: Stewart's Theorem
|url=https://books.google.com/books?id=r3ILAAAAYAAJ|oclc= 5259132}}

External links

{{MathWorld|title=Stewart's Theorem|urlname=StewartsTheorem}}
{{PlanetMath|title=Stewart's Theorem|urlname=StewartsTheorem}}

4 : Euclidean plane geometry|Triangle geometry|Articles containing proofs|Theorems in plane geometry

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。