- Substring
- Prefix
- Suffix
- Border
- Superstring
- See also
- References
- External links
A substring is a contiguous sequence of characters within a string. For instance, "the best of" is a substring of "It was the best of times". This is not to be confused with subsequence, which is a generalization of substring. For example, "Itwastimes" is a subsequence of "It was the best of times", but not a substring.
Prefix and suffix are special cases of substring. A prefix of a string  is a substring of
is a substring of  that occurs at the beginning of
that occurs at the beginning of  . A suffix of a string
. A suffix of a string  is a substring that occurs at the end of
is a substring that occurs at the end of  .
.
The list of all substrings of the string "apple" would be "apple", "appl", "pple", "app", "ppl", "ple", "ap", "pp", "pl", "le", "a", "p", "l", "e", "".
Substring
A substring (or factor) of a string 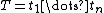 is a string
is a string 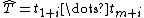 , where
, where 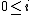 and
and 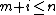 . A substring of a string is a prefix of a suffix of the string, and equivalently a suffix of a prefix. If
. A substring of a string is a prefix of a suffix of the string, and equivalently a suffix of a prefix. If 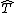 is a substring of
is a substring of 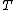 , it is also a subsequence, which is a more general concept. Given a pattern
, it is also a subsequence, which is a more general concept. Given a pattern  , you can find its occurrences in a string
, you can find its occurrences in a string 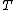 with a string searching algorithm. Finding the longest string which is equal to a substring of two or more strings is known as the longest common substring problem.
with a string searching algorithm. Finding the longest string which is equal to a substring of two or more strings is known as the longest common substring problem.
Example: The string ana is equal to substrings (and subsequences) of banana at two different offsets:
|||||
|||
In the mathematical literature, substrings are also called subwords (in America) or factors (in Europe).
Not including the empty substring, the number of substrings of a string of length  where symbols only occur once, is the number of ways to choose two distinct places between symbols to start/end the substring. Including the very beginning and very end of the string, there are
where symbols only occur once, is the number of ways to choose two distinct places between symbols to start/end the substring. Including the very beginning and very end of the string, there are  such places. So there are
such places. So there are 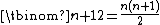 non-empty substrings.
non-empty substrings.
Prefix
{{see also|String operations#Prefixes}}A prefix of a string 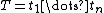 is a string
is a string 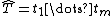 , where
, where 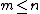 . A proper prefix of a string is not equal to the string itself (
. A proper prefix of a string is not equal to the string itself (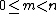 );[1] some sources in addition restrict a proper prefix to be non-empty (
);[1] some sources in addition restrict a proper prefix to be non-empty (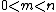 ). A prefix can be seen as a special case of a substring.
). A prefix can be seen as a special case of a substring.
Example: The string ban is equal to a prefix (and substring and subsequence) of the string banana:
|||
The square subset symbol is sometimes used to indicate a prefix, so that 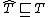 denotes that
denotes that 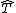 is a prefix of
is a prefix of 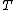 . This defines a binary relation on strings, called the prefix relation, which is a particular kind of prefix order.
. This defines a binary relation on strings, called the prefix relation, which is a particular kind of prefix order.
In formal language theory, the term prefix of a string is also commonly understood to be the set of all prefixes of a string, with respect to that language.
Suffix
A suffix of a string is any substring of the string which includes its last letter, including itself. A proper suffix of a string is not equal to the string itself. A more restricted interpretation is that it is also not empty{{ref|Gus97}}. A suffix can be seen as a special case of a substring.
Example: The string nana is equal to a suffix (and substring and subsequence) of the string banana:
||||
A suffix tree for a string is a trie data structure that represents all of its suffixes. Suffix trees have large numbers of applications in string algorithms. The suffix array is a simplified version of this data structure that lists the start positions of the suffixes in alphabetically sorted order; it has many of the same applications.
Border
A border is suffix and prefix of the same string, e.g. "bab" is a border of "babab" (and also of "babooneatingakebab").
Superstring
Given a set of  strings
strings  , a superstring of the set
, a superstring of the set  is a single string that contains every string in
is a single string that contains every string in  as a substring. For example, a concatenation of the strings of
as a substring. For example, a concatenation of the strings of  in any order gives a trivial superstring of
in any order gives a trivial superstring of  . For a more interesting example, let
. For a more interesting example, let 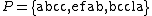 . Then
. Then 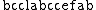 is a superstring of
is a superstring of  , and
, and 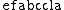 is another, shorter superstring of
is another, shorter superstring of  . Generally, we are interested in finding superstrings whose length is small.{{Clarify|reason=why are we interested in them?|date=June 2010}}
. Generally, we are interested in finding superstrings whose length is small.{{Clarify|reason=why are we interested in them?|date=June 2010}}
See also
- Brace notation
- Substring index
- Suffix automaton
References
}}
External links
- {{Commonscatinline}}
- List of members of the National Assembly of Zambia (1996–2001)
- List of members of the National Assembly of Zambia (2002-06)
- List of members of the National Assembly of Zambia (2002–06)
- List of members of the National Assembly of Zambia (2006-11)
- List of members of the National Assembly of Zambia (2006–11)
- List of members of the National Assembly of Zambia (2011-16)
- List of members of the National Assembly of Zambia (2011–16)
- List of members of the National Assembly of Zambia (2016-21)
- List of members of the National Assembly of Zambia (2016–21)
- List of members of the National Assembly (South Korea), 1950-1954
- List of members of the National Assembly (South Korea), 1950-54
- List of members of the National Assembly (South Korea), 1950–54
- List of members of the National Assembly (South Korea), 2012-
- List of members of the National Assembly (South Korea), 2012-16
- List of members of the National Assembly (South Korea), 2012-2016
- List of members of the National Assembly (South Korea), 2012–
- List of members of the National Assembly (South Korea), 2012–16
- List of members of the National Assembly (South Korea), 2016-2020
- List of members of the National Assembly (South Korea), 2016-present
- List of members of the National Assembly (South Korea), 2016–2020
- List of members of the National Congress of Honduras, 2006-10
- List of members of the National Congress of Honduras, 2010-14
- List of members of the National Council of Slovakia (2012-16)
- List of members of the National Council of Slovakia, 2012-16
- List of members of the National Council of Slovakia, 2012–16