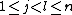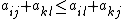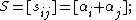“Supnick matrix”的意思、由来-开放百科全书

词条

Supnick matrix

释义

Mathematical definition
Properties
References

A Supnick matrix or Supnick array – named after Fred Supnick of the City College of New York, who introduced the notion in 1957 – is a Monge array which is also a symmetric matrix.

Mathematical definition

A Supnick matrix is a square Monge array that is symmetric around the main diagonal.

An n-by-n matrix is a Supnick matrix if, for all i, j, k, l such that if

and

then

and also

A logically equivalent definition is given by Rudolf & Woeginger who in 1995 proved that

A matrix is a Supnick matrix iff it can be written as the sum of a sum matrix S and a non-negative linear combination of LL-UR block matrices.

The sum matrix is defined in terms of a sequence of n real numbers {α_i}:

and an LL-UR block matrix consists of two symmetrically placed rectangles in the lower-left and upper right corners for which a_ij = 1, with all the rest of the matrix elements equal to zero.

Properties

Adding two Supnick matrices together will result in a new Supnick matrix (Deineko and Woeginger 2006).

Multiplying a Supnick matrix by a non-negative real number produces a new Supnick matrix (Deineko and Woeginger 2006).

If the distance matrix in a traveling salesman problem can be written as a Supnick matrix, that particular instance of the problem admits an easy solution (even though the problem is, in general, NP hard).

References

{{cite journal|last = Supnick|first = Fred|title = Extreme Hamiltonian Lines|journal = Annals of Mathematics |series=Second Series|volume = 66|issue = 1|date = July 1957|pages = 179–201|jstor=1970124}}
{{cite journal|last = Woeginger|first = Gerhard J.| authorlink = Gerhard J. Woeginger |title = Computational Problems without Computation|journal = Nieuwarchief|volume = 5|issue = 4|date = June 2003|pages = 140–147|url = http://www.nieuwarchief.nl/serie5/deel04/jun2003/pdf/woeginger.pdf}}
{{cite journal | title = Some problems around travelling salesmen, dart boards, and euro-coins | first1 = Vladimir G. | last1 = Deineko | first2 = Gerhard J. | last2 = Woeginger | author2-link = Gerhard J. Woeginger | journal = Bulletin of the European Association for Theoretical Computer Science | publisher = EATCS | volume = 90 |date=October 2006 | issn = 0252-9742 | pages = 43–52 | url = http://alexandria.tue.nl/openaccess/Metis211810.pdf | format = PDF }}

2 : Computer science|Matrices

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。