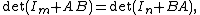“Sylvester's determinant identity”的意思、由来-开放百科全书

In matrix theory, Sylvester's determinant identity is an identity useful for evaluating certain types of determinants. It is named after James Joseph Sylvester, who stated this identity without proof in 1851.^[1]

The identity states that if {{math|A}} and {{math|B}} are matrices of size {{math|m × n}} and {{math|n × m}} respectively, then

It is closely related to the Matrix determinant lemma and its generalization. It is the determinant analogue of the Woodbury matrix identity for matrix inverses.

Proof

The identity may be proved as follows.^[4] Let {{math|M}} be a matrix comprising the four blocks {{math|I_m}}, {{math|−A}}, {{math|B}}, and {{math|I_n}}:

Because {{math|I_m}} is invertible, the formula for the determinant of a block matrix gives

Because {{math|I_n}} is invertible, the formula for the determinant of a block matrix gives

Applications

This identify is useful in developing a Bayes estimator for multivariate Gaussian distributions.

The identity also finds applications in random matrix theory by relating determinants of large matrices to determinants of smaller ones.^[5]

References

1. ^{{cite journal | last = Sylvester | first = James Joseph | title = On the relation between the minor determinants of linearly equivalent quadratic functions | journal = Philosophical Magazine | volume = 1 | year = 1851 | pages = 295–305}}
Cited in {{Cite journal | last1 = Akritas | first1 = A. G. | last2 = Akritas | first2 = E. K. | last3 = Malaschonok | first3 = G. I. | doi = 10.1016/S0378-4754(96)00035-3 | title = Various proofs of Sylvester's (determinant) identity | journal = Mathematics and Computers in Simulation | volume = 42 | issue = 4–6 | page = 585 | year = 1996 | pmid = | pmc = }}
2. ^{{cite book |author=Harville, David A. |title=Matrix algebra from a statistician's perspective |publisher=Springer |location=Berlin |year=2008 |pages= |isbn=0-387-78356-3}} page 416
3. ^{{cite web |last=Weisstein |first=Eric W. |title=Sylvester's Determinant Identity |publisher=MathWorld--A Wolfram Web Resource |url=http://mathworld.wolfram.com/SylvestersDeterminantIdentity.html |accessdate=2012-03-03}}
4. ^{{citation|title=An Introduction to Grids, Graphs, and Networks|first=C.|last=Pozrikidis|publisher=Oxford University Press|year=2014|isbn=9780199996735|page=271|url=https://books.google.com/books?id=Ws_RAgAAQBAJ&pg=PA271}}
5. ^{{cite web|url=http://terrytao.wordpress.com/2010/12/17/the-mesoscopic-structure-of-gue-eigenvalues/ |title=The mesoscopic structure of GUE eigenvalues | What's new |website=Terrytao.wordpress.com |date= |accessdate=2016-01-16}}