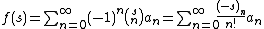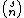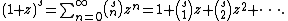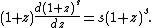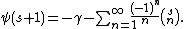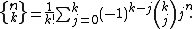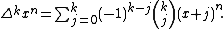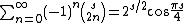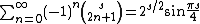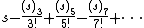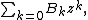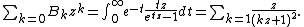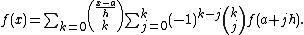“Table of Newtonian series”的意思、由来-开放百科全书

词条

Table of Newtonian series

释义

List
See also
References

In mathematics, a Newtonian series, named after Isaac Newton, is a sum over a sequence written in the form

where

is the binomial coefficient and 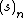is the rising factorial. Newtonian series often appear in relations of the form seen in umbral calculus.

List

The generalized binomial theorem gives

A proof for this identity can be obtained by showing that it satisfies the differential equation

The digamma function:

The Stirling numbers of the second kind are given by the finite sum

This formula is a special case of the kth forward difference of the monomial xⁿ evaluated at x = 0:

A related identity forms the basis of the Nörlund–Rice integral:

where 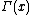is the Gamma function and is the Beta function.

The trigonometric functions have umbral identities:

and

The umbral nature of these identities is a bit more clear by writing them in terms of the falling factorial 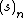. The first few terms of the sin series are

which can be recognized as resembling the Taylor series for sin x, with (s)_n standing in the place of xⁿ.

In analytic number theory it is of interest to sum

where B are the Bernoulli numbers. Employing the generating function its Borel sum can be evaluated as

The general relation gives the Newton series

{{Citation needed|date=February 2012}}

where is the Hurwitz zeta function and 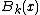the Bernoulli polynomial. The series does not converge, the identity holds formally.

Another identity is

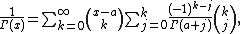
which converges for 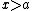. This follows from the general form of a Newton series for equidistant nodes (when it exists, i.e. is convergent)

References

Philippe Flajolet and Robert Sedgewick, "Mellin transforms and asymptotics: Finite differences and Rice's integrals{{Dead link|date=June 2018 |bot=InternetArchiveBot |fix-attempted=no }}", Theoretical Computer Science 144 (1995) pp 101–124.

3 : Finite differences|Factorial and binomial topics|Mathematics-related lists

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。

List

See also

References