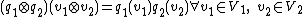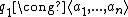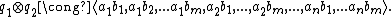“Tensor product of quadratic forms”的意思、由来-开放百科全书

词条

Tensor product of quadratic forms

释义

The tensor product of quadratic forms is most easily understood when one views the quadratic forms as quadratic spaces. If R is a commutative ring where 2 is invertible, and if and 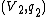are two quadratic spaces over R, then their tensor product 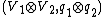is the quadratic space whose underlying R-module is the tensor product of R-modules and whose quadratic form is the quadratic form associated to the tensor product of the bilinear forms associated to 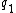and .

In particular, the form 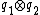satisfies

(which does uniquely characterize it however). It follow from this that if we have diagonalizations of our quadratic forms (which is always possible if 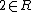is invertible) such that

then the tensor product has diagonalization

2 : Quadratic forms|Tensors

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。