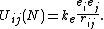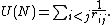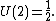- Mathematical statement Example
- Known solutions
- Generalizations
- Relations to other scientific problems
- Configurations of smallest known energy
- References
- Notes
The objective of the Thomson problem is to determine the minimum electrostatic potential energy configuration of N electrons constrained to the surface of a unit sphere that repel each other with a force given by Coulomb's law. The physicist J. J. Thomson posed the problem in 1904[1] after proposing an atomic model, later called the plum pudding model, based on his knowledge of the existence of negatively charged electrons within neutrally-charged atoms.
Related problems include the study of the geometry of the minimum energy configuration and the study of the large N behavior of the minimum energy.
Mathematical statement
The physical system embodied by the Thomson problem is a special case of one of eighteen unsolved mathematics problems proposed by the mathematician Steve Smale — "Distribution of points on the 2-sphere".[2] The solution of each N-electron problem is obtained when the N-electron configuration constrained to the surface of a sphere of unit radius, 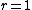 , yields a global electrostatic potential energy minimum,
, yields a global electrostatic potential energy minimum, 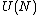 .
.
The electrostatic interaction energy occurring between each pair of electrons of equal charges (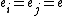 , with
, with  the elementary charge of an electron) is given by Coulomb's Law,
the elementary charge of an electron) is given by Coulomb's Law,
Here,  is Coulomb's constant and
is Coulomb's constant and 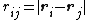 is the distance between each pair of electrons located at points on the sphere defined by vectors
is the distance between each pair of electrons located at points on the sphere defined by vectors  and
and 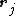 , respectively.
, respectively.
Simplified units of  and
and 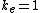 are used without loss of generality. Then,
are used without loss of generality. Then,
The total electrostatic potential energy of each N-electron configuration may then be expressed as the sum of all pair-wise interactions
The global minimization of 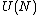 over all possible collections of N distinct points is typically found by numerical minimization algorithms.
over all possible collections of N distinct points is typically found by numerical minimization algorithms.
Example
The solution of the Thomson problem for two electrons is obtained when both electrons are as far apart as possible on opposite sides of the origin, 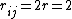 , or
, or
Known solutions
Minimum energy configurations have been rigorously identified in only a handful of cases.
- For N = 1, the solution is trivial as the electron may reside at any point on the surface of the unit sphere. The total energy of the configuration is defined as zero as the electron is not subject to the electric field due to any other sources of charge.
- For N = 2, the optimal configuration consists of electrons at antipodal points.
- For N = 3, electrons reside at the vertices of an equilateral triangle about a great circle.[3]
- For N = 4, electrons reside at the vertices of a regular tetrahedron.
- For N = 5, a mathematically rigorous computer-aided solution was reported in 2010 with electrons residing at vertices of a triangular dipyramid.[4]
- For N = 6, electrons reside at vertices of a regular octahedron.[5]
- For N = 12, electrons reside at the vertices of a regular icosahedron.[6]
Notably, the geometric solutions of the Thomson problem for N = 4, 6, and 12 electrons are known as Platonic solids whose faces are all congruent equilateral triangles. Numerical solutions for N = 8 and 20 are not the regular convex polyhedral configurations of the remaining two Platonic solids, whose faces are square and pentagonal, respectively.
Generalizations
One can also ask for ground states of particles interacting with arbitrary potentials.
To be mathematically precise, let f be a decreasing real-valued function, and define the energy functional 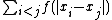
Traditionally, one considers 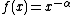 also known as Riesz
also known as Riesz  -kernels. For integrable Riesz kernels see;[7] for non-integrable Riesz kernels, the Poppy-seed bagel theorem holds, see.[8] Notable cases include α = ∞, the Tammes problem (packing); α = 1, the Thomson problem; α = 0, Whyte's problem (to maximize the product of distances).
-kernels. For integrable Riesz kernels see;[7] for non-integrable Riesz kernels, the Poppy-seed bagel theorem holds, see.[8] Notable cases include α = ∞, the Tammes problem (packing); α = 1, the Thomson problem; α = 0, Whyte's problem (to maximize the product of distances).
One may also consider configurations of N points on a sphere of higher dimension. See spherical design.
Relations to other scientific problems
The Thomson problem is a natural consequence of Thomson's plum pudding model in the absence of its uniform positive background charge.[9]
{{quote box|width=23em|"No fact discovered about the atom can be trivial, nor fail to accelerate the progress of physical science, for the greater part of natural philosophy is the outcome of the structure and mechanism of the atom."|—Sir J. J. Thomson[10]}}Though experimental evidence led to the abandonment of Thomson's plum pudding model as a complete atomic model, irregularities observed in numerical energy solutions of the Thomson problem have been found to correspond with electron shell-filling in naturally occurring atoms throughout the periodic table of elements.[11]
The Thomson problem also plays a role in the study of other physical models including multi-electron bubbles and the surface ordering of liquid metal drops confined in Paul traps.
The generalized Thomson problem arises, for example, in determining the arrangements of the protein subunits which comprise the shells of spherical viruses. The "particles" in this application are clusters of protein subunits arranged on a shell. Other realizations include regular arrangements of colloid particles in colloidosomes, proposed for encapsulation of active ingredients such as drugs, nutrients or living cells, fullerene patterns of carbon atoms, and VSEPR theory. An example with long-range logarithmic interactions is provided by the Abrikosov vortices which would form at low temperatures in a superconducting metal shell with a large monopole at the center.
Configurations of smallest known energy
In the following table  is the number of points (charges) in a configuration,
is the number of points (charges) in a configuration,  is the energy, the symmetry type is given in Schönflies notation (see Point groups in three dimensions), and
is the energy, the symmetry type is given in Schönflies notation (see Point groups in three dimensions), and  are the positions of the charges. Most symmetry types require the vector sum of the positions (and thus the electric dipole moment) to be zero.
are the positions of the charges. Most symmetry types require the vector sum of the positions (and thus the electric dipole moment) to be zero.
It is customary to also consider the polyhedron formed by the convex hull of the points. Thus,  is the number of vertices where the given number of edges meet, '
is the number of vertices where the given number of edges meet, ' is the total number of edges,
is the total number of edges,  is the number of triangular faces,
is the number of triangular faces, 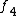 is the number of quadrilateral faces, and
is the number of quadrilateral faces, and 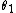 is the smallest angle subtended by vectors associated with the nearest charge pair. Note that the edge lengths are generally not equal; thus (except in the cases N = 4, 6, 12, 24) the convex hull is only topologically equivalent to the uniform polyhedron or Johnson solid listed in the last column.[12]
is the smallest angle subtended by vectors associated with the nearest charge pair. Note that the edge lengths are generally not equal; thus (except in the cases N = 4, 6, 12, 24) the convex hull is only topologically equivalent to the uniform polyhedron or Johnson solid listed in the last column.[12]
| N | 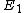 | Symmetry | 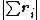 | 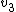 | 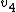 |  | 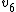 | 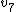 | 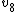 |  |  | 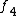 | 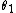 | Equivalent polyhedron |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 2 | 0.500000000 |  | 0 | – | – | – | – | – | – | 1 | – | – | 180.000° | digon |
| 3 | 1.732050808 |  | 0 | – | – | – | – | – | – | 3 | 1 | – | 120.000° | triangle |
| 4 | 3.674234614 | 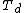 | 0 | 4 | 0 | 0 | 0 | 0 | 0 | 6 | 4 | 0 | 109.471° | tetrahedron |
| 5 | 6.474691495 |  | 0 | 2 | 3 | 0 | 0 | 0 | 0 | 9 | 6 | 0 | 90.000° | triangular dipyramid |
| 6 | 9.985281374 | 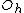 | 0 | 0 | 6 | 0 | 0 | 0 | 0 | 12 | 8 | 0 | 90.000° | octahedron |
| 7 | 14.452977414 | 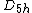 | 0 | 0 | 5 | 2 | 0 | 0 | 0 | 15 | 10 | 0 | 72.000° | pentagonal dipyramid |
| 8 | 19.675287861 | 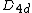 | 0 | 0 | 8 | 0 | 0 | 0 | 0 | 16 | 8 | 2 | 71.694° | square antiprism |
| 9 | 25.759986531 |  | 0 | 0 | 3 | 6 | 0 | 0 | 0 | 21 | 14 | 0 | 69.190° | triaugmented triangular prism |
| 10 | 32.716949460 | 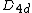 | 0 | 0 | 2 | 8 | 0 | 0 | 0 | 24 | 16 | 0 | 64.996° | gyroelongated square dipyramid |
| 11 | 40.596450510 | 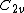 | 0.013219635 | 0 | 2 | 8 | 1 | 0 | 0 | 27 | 18 | 0 | 58.540° | edge-contracted icosahedron |
| 12 | 49.165253058 | 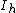 | 0 | 0 | 0 | 12 | 0 | 0 | 0 | 30 | 20 | 0 | 63.435° | icosahedron |
| 13 | 58.853230612 | 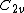 | 0.008820367 | 0 | 1 | 10 | 2 | 0 | 0 | 33 | 22 | 0 | 52.317° | |
| 14 | 69.306363297 | 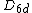 | 0 | 0 | 0 | 12 | 2 | 0 | 0 | 36 | 24 | 0 | 52.866° | gyroelongated hexagonal dipyramid |
| 15 | 80.670244114 |  | 0 | 0 | 0 | 12 | 3 | 0 | 0 | 39 | 26 | 0 | 49.225° | |
| 16 | 92.911655302 | 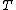 | 0 | 0 | 0 | 12 | 4 | 0 | 0 | 42 | 28 | 0 | 48.936° | |
| 17 | 106.050404829 | 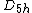 | 0 | 0 | 0 | 12 | 5 | 0 | 0 | 45 | 30 | 0 | 50.108° | |
| 18 | 120.084467447 | 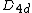 | 0 | 0 | 2 | 8 | 8 | 0 | 0 | 48 | 32 | 0 | 47.534° | |
| 19 | 135.089467557 | 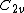 | 0.000135163 | 0 | 0 | 14 | 5 | 0 | 0 | 50 | 32 | 1 | 44.910° | |
| 20 | 150.881568334 |  | 0 | 0 | 0 | 12 | 8 | 0 | 0 | 54 | 36 | 0 | 46.093° | |
| 21 | 167.641622399 | 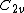 | 0.001406124 | 0 | 1 | 10 | 10 | 0 | 0 | 57 | 38 | 0 | 44.321° | |
| 22 | 185.287536149 | 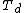 | 0 | 0 | 0 | 12 | 10 | 0 | 0 | 60 | 40 | 0 | 43.302° | |
| 23 | 203.930190663 |  | 0 | 0 | 0 | 12 | 11 | 0 | 0 | 63 | 42 | 0 | 41.481° | |
| 24 | 223.347074052 |  | 0 | 0 | 0 | 24 | 0 | 0 | 0 | 60 | 32 | 6 | 42.065° | snub cube |
| 25 | 243.812760299 |  | 0.001021305 | 0 | 0 | 14 | 11 | 0 | 0 | 68 | 44 | 1 | 39.610° | |
| 26 | 265.133326317 |  | 0.001919065 | 0 | 0 | 12 | 14 | 0 | 0 | 72 | 48 | 0 | 38.842° | |
| 27 | 287.302615033 | 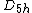 | 0 | 0 | 0 | 12 | 15 | 0 | 0 | 75 | 50 | 0 | 39.940° | |
| 28 | 310.491542358 | 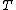 | 0 | 0 | 0 | 12 | 16 | 0 | 0 | 78 | 52 | 0 | 37.824° | |
| 29 | 334.634439920 |  | 0 | 0 | 0 | 12 | 17 | 0 | 0 | 81 | 54 | 0 | 36.391° | |
| 30 | 359.603945904 | 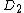 | 0 | 0 | 0 | 12 | 18 | 0 | 0 | 84 | 56 | 0 | 36.942° | |
| 31 | 385.530838063 |  | 0.003204712 | 0 | 0 | 12 | 19 | 0 | 0 | 87 | 58 | 0 | 36.373° | |
| 32 | 412.261274651 | 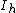 | 0 | 0 | 0 | 12 | 20 | 0 | 0 | 90 | 60 | 0 | 37.377° | |
| 33 | 440.204057448 |  | 0.004356481 | 0 | 0 | 15 | 17 | 1 | 0 | 92 | 60 | 1 | 33.700° | |
| 34 | 468.904853281 | 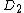 | 0 | 0 | 0 | 12 | 22 | 0 | 0 | 96 | 64 | 0 | 33.273° | |
| 35 | 498.569872491 |  | 0.000419208 | 0 | 0 | 12 | 23 | 0 | 0 | 99 | 66 | 0 | 33.100° | |
| 36 | 529.122408375 | 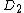 | 0 | 0 | 0 | 12 | 24 | 0 | 0 | 102 | 68 | 0 | 33.229° | |
| 37 | 560.618887731 | 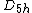 | 0 | 0 | 0 | 12 | 25 | 0 | 0 | 105 | 70 | 0 | 32.332° | |
| 38 | 593.038503566 | 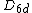 | 0 | 0 | 0 | 12 | 26 | 0 | 0 | 108 | 72 | 0 | 33.236° | |
| 39 | 626.389009017 |  | 0 | 0 | 0 | 12 | 27 | 0 | 0 | 111 | 74 | 0 | 32.053° | |
| 40 | 660.675278835 | 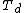 | 0 | 0 | 0 | 12 | 28 | 0 | 0 | 114 | 76 | 0 | 31.916° | |
| 41 | 695.916744342 |  | 0 | 0 | 0 | 12 | 29 | 0 | 0 | 117 | 78 | 0 | 31.528° | |
| 42 | 732.078107544 | 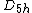 | 0 | 0 | 0 | 12 | 30 | 0 | 0 | 120 | 80 | 0 | 31.245° | |
| 43 | 769.190846459 | 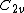 | 0.000399668 | 0 | 0 | 12 | 31 | 0 | 0 | 123 | 82 | 0 | 30.867° | |
| 44 | 807.174263085 | 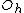 | 0 | 0 | 0 | 24 | 20 | 0 | 0 | 120 | 72 | 6 | 31.258° | |
| 45 | 846.188401061 |  | 0 | 0 | 0 | 12 | 33 | 0 | 0 | 129 | 86 | 0 | 30.207° | |
| 46 | 886.167113639 | 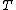 | 0 | 0 | 0 | 12 | 34 | 0 | 0 | 132 | 88 | 0 | 29.790° | |
| 47 | 927.059270680 |  | 0.002482914 | 0 | 0 | 14 | 33 | 0 | 0 | 134 | 88 | 1 | 28.787° | |
| 48 | 968.713455344 |  | 0 | 0 | 0 | 24 | 24 | 0 | 0 | 132 | 80 | 6 | 29.690° | |
| 49 | 1011.557182654 |  | 0.001529341 | 0 | 0 | 12 | 37 | 0 | 0 | 141 | 94 | 0 | 28.387° | |
| 50 | 1055.182314726 | 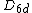 | 0 | 0 | 0 | 12 | 38 | 0 | 0 | 144 | 96 | 0 | 29.231° | |
| 51 | 1099.819290319 |  | 0 | 0 | 0 | 12 | 39 | 0 | 0 | 147 | 98 | 0 | 28.165° | |
| 52 | 1145.418964319 |  | 0.000457327 | 0 | 0 | 12 | 40 | 0 | 0 | 150 | 100 | 0 | 27.670° | |
| 53 | 1191.922290416 | 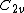 | 0.000278469 | 0 | 0 | 18 | 35 | 0 | 0 | 150 | 96 | 3 | 27.137° | |
| 54 | 1239.361474729 |  | 0.000137870 | 0 | 0 | 12 | 42 | 0 | 0 | 156 | 104 | 0 | 27.030° | |
| 55 | 1287.772720783 |  | 0.000391696 | 0 | 0 | 12 | 43 | 0 | 0 | 159 | 106 | 0 | 26.615° | |
| 56 | 1337.094945276 | 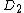 | 0 | 0 | 0 | 12 | 44 | 0 | 0 | 162 | 108 | 0 | 26.683° | |
| 57 | 1387.383229253 |  | 0 | 0 | 0 | 12 | 45 | 0 | 0 | 165 | 110 | 0 | 26.702° | |
| 58 | 1438.618250640 | 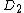 | 0 | 0 | 0 | 12 | 46 | 0 | 0 | 168 | 112 | 0 | 26.155° | |
| 59 | 1490.773335279 |  | 0.000154286 | 0 | 0 | 14 | 43 | 2 | 0 | 171 | 114 | 0 | 26.170° | |
| 60 | 1543.830400976 |  | 0 | 0 | 0 | 12 | 48 | 0 | 0 | 174 | 116 | 0 | 25.958° | |
| 61 | 1597.941830199 |  | 0.001091717 | 0 | 0 | 12 | 49 | 0 | 0 | 177 | 118 | 0 | 25.392° | |
| 62 | 1652.909409898 | 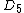 | 0 | 0 | 0 | 12 | 50 | 0 | 0 | 180 | 120 | 0 | 25.880° | |
| 63 | 1708.879681503 |  | 0 | 0 | 0 | 12 | 51 | 0 | 0 | 183 | 122 | 0 | 25.257° | |
| 64 | 1765.802577927 | 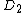 | 0 | 0 | 0 | 12 | 52 | 0 | 0 | 186 | 124 | 0 | 24.920° | |
| 65 | 1823.667960264 |  | 0.000399515 | 0 | 0 | 12 | 53 | 0 | 0 | 189 | 126 | 0 | 24.527° | |
| 66 | 1882.441525304 |  | 0.000776245 | 0 | 0 | 12 | 54 | 0 | 0 | 192 | 128 | 0 | 24.765° | |
| 67 | 1942.122700406 | 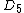 | 0 | 0 | 0 | 12 | 55 | 0 | 0 | 195 | 130 | 0 | 24.727° | |
| 68 | 2002.874701749 | 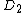 | 0 | 0 | 0 | 12 | 56 | 0 | 0 | 198 | 132 | 0 | 24.433° | |
| 69 | 2064.533483235 |  | 0 | 0 | 0 | 12 | 57 | 0 | 0 | 201 | 134 | 0 | 24.137° | |
| 70 | 2127.100901551 | 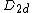 | 0 | 0 | 0 | 12 | 50 | 0 | 0 | 200 | 128 | 4 | 24.291° | |
| 71 | 2190.649906425 |  | 0.001256769 | 0 | 0 | 14 | 55 | 2 | 0 | 207 | 138 | 0 | 23.803° | |
| 72 | 2255.001190975 |  | 0 | 0 | 0 | 12 | 60 | 0 | 0 | 210 | 140 | 0 | 24.492° | |
| 73 | 2320.633883745 |  | 0.001572959 | 0 | 0 | 12 | 61 | 0 | 0 | 213 | 142 | 0 | 22.810° | |
| 74 | 2387.072981838 |  | 0.000641539 | 0 | 0 | 12 | 62 | 0 | 0 | 216 | 144 | 0 | 22.966° | |
| 75 | 2454.369689040 |  | 0 | 0 | 0 | 12 | 63 | 0 | 0 | 219 | 146 | 0 | 22.736° | |
| 76 | 2522.674871841 |  | 0.000943474 | 0 | 0 | 12 | 64 | 0 | 0 | 222 | 148 | 0 | 22.886° | |
| 77 | 2591.850152354 | 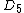 | 0 | 0 | 0 | 12 | 65 | 0 | 0 | 225 | 150 | 0 | 23.286° | |
| 78 | 2662.046474566 |  | 0 | 0 | 0 | 12 | 66 | 0 | 0 | 228 | 152 | 0 | 23.426° | |
| 79 | 2733.248357479 | 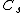 | 0.000702921 | 0 | 0 | 12 | 63 | 1 | 0 | 230 | 152 | 1 | 22.636° | |
| 80 | 2805.355875981 | 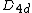 | 0 | 0 | 0 | 16 | 64 | 0 | 0 | 232 | 152 | 2 | 22.778° | |
| 81 | 2878.522829664 |  | 0.000194289 | 0 | 0 | 12 | 69 | 0 | 0 | 237 | 158 | 0 | 21.892° | |
| 82 | 2952.569675286 | 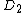 | 0 | 0 | 0 | 12 | 70 | 0 | 0 | 240 | 160 | 0 | 22.206° | |
| 83 | 3027.528488921 |  | 0.000339815 | 0 | 0 | 14 | 67 | 2 | 0 | 243 | 162 | 0 | 21.646° | |
| 84 | 3103.465124431 |  | 0.000401973 | 0 | 0 | 12 | 72 | 0 | 0 | 246 | 164 | 0 | 21.513° | |
| 85 | 3180.361442939 |  | 0.000416581 | 0 | 0 | 12 | 73 | 0 | 0 | 249 | 166 | 0 | 21.498° | |
| 86 | 3258.211605713 |  | 0.001378932 | 0 | 0 | 12 | 74 | 0 | 0 | 252 | 168 | 0 | 21.522° | |
| 87 | 3337.000750014 |  | 0.000754863 | 0 | 0 | 12 | 75 | 0 | 0 | 255 | 170 | 0 | 21.456° | |
| 88 | 3416.720196758 | 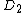 | 0 | 0 | 0 | 12 | 76 | 0 | 0 | 258 | 172 | 0 | 21.486° | |
| 89 | 3497.439018625 |  | 0.000070891 | 0 | 0 | 12 | 77 | 0 | 0 | 261 | 174 | 0 | 21.182° | |
| 90 | 3579.091222723 |  | 0 | 0 | 0 | 12 | 78 | 0 | 0 | 264 | 176 | 0 | 21.230° | |
| 91 | 3661.713699320 |  | 0.000033221 | 0 | 0 | 12 | 79 | 0 | 0 | 267 | 178 | 0 | 21.105° | |
| 92 | 3745.291636241 | 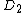 | 0 | 0 | 0 | 12 | 80 | 0 | 0 | 270 | 180 | 0 | 21.026° | |
| 93 | 3829.844338421 |  | 0.000213246 | 0 | 0 | 12 | 81 | 0 | 0 | 273 | 182 | 0 | 20.751° | |
| 94 | 3915.309269620 | 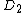 | 0 | 0 | 0 | 12 | 82 | 0 | 0 | 276 | 184 | 0 | 20.952° | |
| 95 | 4001.771675565 |  | 0.000116638 | 0 | 0 | 12 | 83 | 0 | 0 | 279 | 186 | 0 | 20.711° | |
| 96 | 4089.154010060 |  | 0.000036310 | 0 | 0 | 12 | 84 | 0 | 0 | 282 | 188 | 0 | 20.687° | |
| 97 | 4177.533599622 |  | 0.000096437 | 0 | 0 | 12 | 85 | 0 | 0 | 285 | 190 | 0 | 20.450° | |
| 98 | 4266.822464156 |  | 0.000112916 | 0 | 0 | 12 | 86 | 0 | 0 | 288 | 192 | 0 | 20.422° | |
| 99 | 4357.139163132 |  | 0.000156508 | 0 | 0 | 12 | 87 | 0 | 0 | 291 | 194 | 0 | 20.284° | |
| 100 | 4448.350634331 | 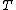 | 0 | 0 | 0 | 12 | 88 | 0 | 0 | 294 | 196 | 0 | 20.297° | |
| 101 | 4540.590051694 |  | 0 | 0 | 0 | 12 | 89 | 0 | 0 | 297 | 198 | 0 | 20.011° | |
| 102 | 4633.736565899 |  | 0 | 0 | 0 | 12 | 90 | 0 | 0 | 300 | 200 | 0 | 20.040° | |
| 103 | 4727.836616833 |  | 0.000201245 | 0 | 0 | 12 | 91 | 0 | 0 | 303 | 202 | 0 | 19.907° | |
| 104 | 4822.876522746 | 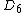 | 0 | 0 | 0 | 12 | 92 | 0 | 0 | 306 | 204 | 0 | 19.957° | |
| 105 | 4919.000637616 |  | 0 | 0 | 0 | 12 | 93 | 0 | 0 | 309 | 206 | 0 | 19.842° | |
| 106 | 5015.984595705 | 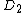 | 0 | 0 | 0 | 12 | 94 | 0 | 0 | 312 | 208 | 0 | 19.658° | |
| 107 | 5113.953547724 |  | 0.000064137 | 0 | 0 | 12 | 95 | 0 | 0 | 315 | 210 | 0 | 19.327° | |
| 108 | 5212.813507831 |  | 0.000432525 | 0 | 0 | 12 | 96 | 0 | 0 | 318 | 212 | 0 | 19.327° | |
| 109 | 5312.735079920 |  | 0.000647299 | 0 | 0 | 14 | 93 | 2 | 0 | 321 | 214 | 0 | 19.103° | |
| 110 | 5413.549294192 | 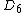 | 0 | 0 | 0 | 12 | 98 | 0 | 0 | 324 | 216 | 0 | 19.476° | |
| 111 | 5515.293214587 |  | 0 | 0 | 0 | 12 | 99 | 0 | 0 | 327 | 218 | 0 | 19.255° | |
| 112 | 5618.044882327 | 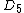 | 0 | 0 | 0 | 12 | 100 | 0 | 0 | 330 | 220 | 0 | 19.351° | |
| 113 | 5721.824978027 |  | 0 | 0 | 0 | 12 | 101 | 0 | 0 | 333 | 222 | 0 | 18.978° | |
| 114 | 5826.521572163 |  | 0.000149772 | 0 | 0 | 12 | 102 | 0 | 0 | 336 | 224 | 0 | 18.836° | |
| 115 | 5932.181285777 | 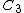 | 0.000049972 | 0 | 0 | 12 | 103 | 0 | 0 | 339 | 226 | 0 | 18.458° | |
| 116 | 6038.815593579 |  | 0.000259726 | 0 | 0 | 12 | 104 | 0 | 0 | 342 | 228 | 0 | 18.386° | |
| 117 | 6146.342446579 |  | 0.000127609 | 0 | 0 | 12 | 105 | 0 | 0 | 345 | 230 | 0 | 18.566° | |
| 118 | 6254.877027790 |  | 0.000332475 | 0 | 0 | 12 | 106 | 0 | 0 | 348 | 232 | 0 | 18.455° | |
| 119 | 6364.347317479 |  | 0.000685590 | 0 | 0 | 12 | 107 | 0 | 0 | 351 | 234 | 0 | 18.336° | |
| 120 | 6474.756324980 | 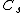 | 0.001373062 | 0 | 0 | 12 | 108 | 0 | 0 | 354 | 236 | 0 | 18.418° | |
| 121 | 6586.121949584 | 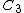 | 0.000838863 | 0 | 0 | 12 | 109 | 0 | 0 | 357 | 238 | 0 | 18.199° | |
| 122 | 6698.374499261 | 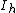 | 0 | 0 | 0 | 12 | 110 | 0 | 0 | 360 | 240 | 0 | 18.612° | |
| 123 | 6811.827228174 | 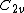 | 0.001939754 | 0 | 0 | 14 | 107 | 2 | 0 | 363 | 242 | 0 | 17.840° | |
| 124 | 6926.169974193 | 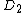 | 0 | 0 | 0 | 12 | 112 | 0 | 0 | 366 | 244 | 0 | 18.111° | |
| 125 | 7041.473264023 |  | 0.000088274 | 0 | 0 | 12 | 113 | 0 | 0 | 369 | 246 | 0 | 17.867° | |
| 126 | 7157.669224867 | 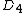 | 0 | 0 | 2 | 16 | 100 | 8 | 0 | 372 | 248 | 0 | 17.920° | |
| 127 | 7274.819504675 | 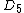 | 0 | 0 | 0 | 12 | 115 | 0 | 0 | 375 | 250 | 0 | 17.877° | |
| 128 | 7393.007443068 |  | 0.000054132 | 0 | 0 | 12 | 116 | 0 | 0 | 378 | 252 | 0 | 17.814° | |
| 129 | 7512.107319268 |  | 0.000030099 | 0 | 0 | 12 | 117 | 0 | 0 | 381 | 254 | 0 | 17.743° | |
| 130 | 7632.167378912 |  | 0.000025622 | 0 | 0 | 12 | 118 | 0 | 0 | 384 | 256 | 0 | 17.683° | |
| 131 | 7753.205166941 |  | 0.000305133 | 0 | 0 | 12 | 119 | 0 | 0 | 387 | 258 | 0 | 17.511° | |
| 132 | 7875.045342797 |  | 0 | 0 | 0 | 12 | 120 | 0 | 0 | 390 | 260 | 0 | 17.958° | |
| 133 | 7998.179212898 | 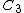 | 0.000591438 | 0 | 0 | 12 | 121 | 0 | 0 | 393 | 262 | 0 | 17.133° | |
| 134 | 8122.089721194 |  | 0.000470268 | 0 | 0 | 12 | 122 | 0 | 0 | 396 | 264 | 0 | 17.214° | |
| 135 | 8246.909486992 |  | 0 | 0 | 0 | 12 | 123 | 0 | 0 | 399 | 266 | 0 | 17.431° | |
| 136 | 8372.743302539 | 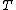 | 0 | 0 | 0 | 12 | 124 | 0 | 0 | 402 | 268 | 0 | 17.485° | |
| 137 | 8499.534494782 | 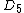 | 0 | 0 | 0 | 12 | 125 | 0 | 0 | 405 | 270 | 0 | 17.560° | |
| 138 | 8627.406389880 |  | 0.000473576 | 0 | 0 | 12 | 126 | 0 | 0 | 408 | 272 | 0 | 16.924° | |
| 139 | 8756.227056057 |  | 0.000404228 | 0 | 0 | 12 | 127 | 0 | 0 | 411 | 274 | 0 | 16.673° | |
| 140 | 8885.980609041 |  | 0.000630351 | 0 | 0 | 13 | 126 | 1 | 0 | 414 | 276 | 0 | 16.773° | |
| 141 | 9016.615349190 | 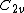 | 0.000376365 | 0 | 0 | 14 | 126 | 0 | 1 | 417 | 278 | 0 | 16.962° | |
| 142 | 9148.271579993 |  | 0.000550138 | 0 | 0 | 12 | 130 | 0 | 0 | 420 | 280 | 0 | 16.840° | |
| 143 | 9280.839851192 |  | 0.000255449 | 0 | 0 | 12 | 131 | 0 | 0 | 423 | 282 | 0 | 16.782° | |
| 144 | 9414.371794460 | 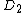 | 0 | 0 | 0 | 12 | 132 | 0 | 0 | 426 | 284 | 0 | 16.953° | |
| 145 | 9548.928837232 | 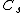 | 0.000094938 | 0 | 0 | 12 | 133 | 0 | 0 | 429 | 286 | 0 | 16.841° | |
| 146 | 9684.381825575 | 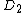 | 0 | 0 | 0 | 12 | 134 | 0 | 0 | 432 | 288 | 0 | 16.905° | |
| 147 | 9820.932378373 |  | 0.000636651 | 0 | 0 | 12 | 135 | 0 | 0 | 435 | 290 | 0 | 16.458° | |
| 148 | 9958.406004270 |  | 0.000203701 | 0 | 0 | 12 | 136 | 0 | 0 | 438 | 292 | 0 | 16.627° | |
| 149 | 10096.859907397 |  | 0.000638186 | 0 | 0 | 14 | 133 | 2 | 0 | 441 | 294 | 0 | 16.344° | |
| 150 | 10236.196436701 | 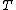 | 0 | 0 | 0 | 12 | 138 | 0 | 0 | 444 | 296 | 0 | 16.405° | |
| 151 | 10376.571469275 |  | 0.000153836 | 0 | 0 | 12 | 139 | 0 | 0 | 447 | 298 | 0 | 16.163° | |
| 152 | 10517.867592878 | 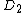 | 0 | 0 | 0 | 12 | 140 | 0 | 0 | 450 | 300 | 0 | 16.117° | |
| 153 | 10660.082748237 |  | 0 | 0 | 0 | 12 | 141 | 0 | 0 | 453 | 302 | 0 | 16.390° | |
| 154 | 10803.372421141 |  | 0.000735800 | 0 | 0 | 12 | 142 | 0 | 0 | 456 | 304 | 0 | 16.078° | |
| 155 | 10947.574692279 |  | 0.000603670 | 0 | 0 | 12 | 143 | 0 | 0 | 459 | 306 | 0 | 15.990° | |
| 156 | 11092.798311456 |  | 0.000508534 | 0 | 0 | 12 | 144 | 0 | 0 | 462 | 308 | 0 | 15.822° | |
| 157 | 11238.903041156 |  | 0.000357679 | 0 | 0 | 12 | 145 | 0 | 0 | 465 | 310 | 0 | 15.948° | |
| 158 | 11385.990186197 |  | 0.000921918 | 0 | 0 | 12 | 146 | 0 | 0 | 468 | 312 | 0 | 15.987° | |
| 159 | 11534.023960956 |  | 0.000381457 | 0 | 0 | 12 | 147 | 0 | 0 | 471 | 314 | 0 | 15.960° | |
| 160 | 11683.054805549 | 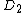 | 0 | 0 | 0 | 12 | 148 | 0 | 0 | 474 | 316 | 0 | 15.961° | |
| 161 | 11833.084739465 |  | 0.000056447 | 0 | 0 | 12 | 149 | 0 | 0 | 477 | 318 | 0 | 15.810° | |
| 162 | 11984.050335814 |  | 0 | 0 | 0 | 12 | 150 | 0 | 0 | 480 | 320 | 0 | 15.813° | |
| 163 | 12136.013053220 |  | 0.000120798 | 0 | 0 | 12 | 151 | 0 | 0 | 483 | 322 | 0 | 15.675° | |
| 164 | 12288.930105320 | 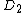 | 0 | 0 | 0 | 12 | 152 | 0 | 0 | 486 | 324 | 0 | 15.655° | |
| 165 | 12442.804451373 |  | 0.000091119 | 0 | 0 | 12 | 153 | 0 | 0 | 489 | 326 | 0 | 15.651° | |
| 166 | 12597.649071323 | 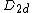 | 0 | 0 | 0 | 16 | 146 | 4 | 0 | 492 | 328 | 0 | 15.607° | |
| 167 | 12753.469429750 |  | 0.000097382 | 0 | 0 | 12 | 155 | 0 | 0 | 495 | 330 | 0 | 15.600° | |
| 168 | 12910.212672268 |  | 0 | 0 | 0 | 12 | 156 | 0 | 0 | 498 | 332 | 0 | 15.655° | |
| 169 | 13068.006451127 | 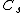 | 0.000068102 | 0 | 0 | 13 | 155 | 1 | 0 | 501 | 334 | 0 | 15.537° | |
| 170 | 13226.681078541 | 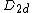 | 0 | 0 | 0 | 12 | 158 | 0 | 0 | 504 | 336 | 0 | 15.569° | |
| 171 | 13386.355930717 |  | 0 | 0 | 0 | 12 | 159 | 0 | 0 | 507 | 338 | 0 | 15.497° | |
| 172 | 13547.018108787 | 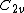 | 0.000547291 | 0 | 0 | 14 | 156 | 2 | 0 | 510 | 340 | 0 | 15.292° | |
| 173 | 13708.635243034 | 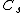 | 0.000286544 | 0 | 0 | 12 | 161 | 0 | 0 | 513 | 342 | 0 | 15.225° | |
| 174 | 13871.187092292 | 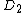 | 0 | 0 | 0 | 12 | 162 | 0 | 0 | 516 | 344 | 0 | 15.366° | |
| 175 | 14034.781306929 |  | 0.000026686 | 0 | 0 | 12 | 163 | 0 | 0 | 519 | 346 | 0 | 15.252° | |
| 176 | 14199.354775632 |  | 0.000283978 | 0 | 0 | 12 | 164 | 0 | 0 | 522 | 348 | 0 | 15.101° | |
| 177 | 14364.837545298 | 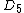 | 0 | 0 | 0 | 12 | 165 | 0 | 0 | 525 | 350 | 0 | 15.269° | |
| 178 | 14531.309552587 | 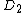 | 0 | 0 | 0 | 12 | 166 | 0 | 0 | 528 | 352 | 0 | 15.145° | |
| 179 | 14698.754594220 |  | 0.000125113 | 0 | 0 | 13 | 165 | 1 | 0 | 531 | 354 | 0 | 14.968° | |
| 180 | 14867.099927525 | 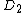 | 0 | 0 | 0 | 12 | 168 | 0 | 0 | 534 | 356 | 0 | 15.067° | |
| 181 | 15036.467239769 |  | 0.000304193 | 0 | 0 | 12 | 169 | 0 | 0 | 537 | 358 | 0 | 15.002° | |
| 182 | 15206.730610906 | 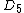 | 0 | 0 | 0 | 12 | 170 | 0 | 0 | 540 | 360 | 0 | 15.155° | |
| 183 | 15378.166571028 |  | 0.000467899 | 0 | 0 | 12 | 171 | 0 | 0 | 543 | 362 | 0 | 14.747° | |
| 184 | 15550.421450311 | 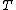 | 0 | 0 | 0 | 12 | 172 | 0 | 0 | 546 | 364 | 0 | 14.932° | |
| 185 | 15723.720074072 |  | 0.000389762 | 0 | 0 | 12 | 173 | 0 | 0 | 549 | 366 | 0 | 14.775° | |
| 186 | 15897.897437048 |  | 0.000389762 | 0 | 0 | 12 | 174 | 0 | 0 | 552 | 368 | 0 | 14.739° | |
| 187 | 16072.975186320 | 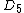 | 0 | 0 | 0 | 12 | 175 | 0 | 0 | 555 | 370 | 0 | 14.848° | |
| 188 | 16249.222678879 | 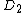 | 0 | 0 | 0 | 12 | 176 | 0 | 0 | 558 | 372 | 0 | 14.740° | |
| 189 | 16426.371938862 |  | 0.000020732 | 0 | 0 | 12 | 177 | 0 | 0 | 561 | 374 | 0 | 14.671° | |
| 190 | 16604.428338501 | 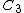 | 0.000586804 | 0 | 0 | 12 | 178 | 0 | 0 | 564 | 376 | 0 | 14.501° | |
| 191 | 16783.452219362 |  | 0.001129202 | 0 | 0 | 13 | 177 | 1 | 0 | 567 | 378 | 0 | 14.195° | |
| 192 | 16963.338386460 |  | 0 | 0 | 0 | 12 | 180 | 0 | 0 | 570 | 380 | 0 | 14.819° | |
| 193 | 17144.564740880 |  | 0.000985192 | 0 | 0 | 12 | 181 | 0 | 0 | 573 | 382 | 0 | 14.144° | |
| 194 | 17326.616136471 |  | 0.000322358 | 0 | 0 | 12 | 182 | 0 | 0 | 576 | 384 | 0 | 14.350° | |
| 195 | 17509.489303930 |  | 0 | 0 | 0 | 12 | 183 | 0 | 0 | 579 | 386 | 0 | 14.375° | |
| 196 | 17693.460548082 |  | 0.000315907 | 0 | 0 | 12 | 184 | 0 | 0 | 582 | 388 | 0 | 14.251° | |
| 197 | 17878.340162571 | 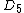 | 0 | 0 | 0 | 12 | 185 | 0 | 0 | 585 | 390 | 0 | 14.147° | |
| 198 | 18064.262177195 |  | 0.000011149 | 0 | 0 | 12 | 186 | 0 | 0 | 588 | 392 | 0 | 14.237° | |
| 199 | 18251.082495640 |  | 0.000534779 | 0 | 0 | 12 | 187 | 0 | 0 | 591 | 394 | 0 | 14.153° | |
| 200 | 18438.842717530 | 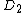 | 0 | 0 | 0 | 12 | 188 | 0 | 0 | 594 | 396 | 0 | 14.222° | |
| 201 | 18627.591226244 |  | 0.001048859 | 0 | 0 | 13 | 187 | 1 | 0 | 597 | 398 | 0 | 13.830° | |
| 202 | 18817.204718262 | 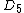 | 0 | 0 | 0 | 12 | 190 | 0 | 0 | 600 | 400 | 0 | 14.189° | |
| 203 | 19007.981204580 | 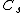 | 0.000600343 | 0 | 0 | 12 | 191 | 0 | 0 | 603 | 402 | 0 | 13.977° | |
| 204 | 19199.540775603 |  | 0 | 0 | 0 | 12 | 192 | 0 | 0 | 606 | 404 | 0 | 14.291° | |
| 212 | 20768.053085964 |  | 0 | 0 | 0 | 12 | 200 | 0 | 0 | 630 | 420 | 0 | 14.118° | |
| 214 | 21169.910410375 | 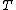 | 0 | 0 | 0 | 12 | 202 | 0 | 0 | 636 | 424 | 0 | 13.771° | |
| 216 | 21575.596377869 |  | 0 | 0 | 0 | 12 | 204 | 0 | 0 | 642 | 428 | 0 | 13.735° | |
| 217 | 21779.856080418 | 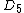 | 0 | 0 | 0 | 12 | 205 | 0 | 0 | 645 | 430 | 0 | 13.902° | |
| 232 | 24961.252318934 | 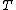 | 0 | 0 | 0 | 12 | 220 | 0 | 0 | 690 | 460 | 0 | 13.260° | |
| 255 | 30264.424251281 |  | 0 | 0 | 0 | 12 | 243 | 0 | 0 | 759 | 506 | 0 | 12.565° | |
| 256 | 30506.687515847 | 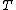 | 0 | 0 | 0 | 12 | 244 | 0 | 0 | 762 | 508 | 0 | 12.572° | |
| 257 | 30749.941417346 | 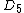 | 0 | 0 | 0 | 12 | 245 | 0 | 0 | 765 | 510 | 0 | 12.672° | |
| 272 | 34515.193292681 | 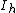 | 0 | 0 | 0 | 12 | 260 | 0 | 0 | 810 | 540 | 0 | 12.335° | |
| 282 | 37147.294418462 |  | 0 | 0 | 0 | 12 | 270 | 0 | 0 | 840 | 560 | 0 | 12.166° | |
| 292 | 39877.008012909 | 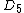 | 0 | 0 | 0 | 12 | 280 | 0 | 0 | 870 | 580 | 0 | 11.857° | |
| 306 | 43862.569780797 |  | 0 | 0 | 0 | 12 | 294 | 0 | 0 | 912 | 608 | 0 | 11.628° | |
| 312 | 45629.313804002 |  | 0.000306163 | 0 | 0 | 12 | 300 | 0 | 0 | 930 | 620 | 0 | 11.299° | |
| 315 | 46525.825643432 |  | 0 | 0 | 0 | 12 | 303 | 0 | 0 | 939 | 626 | 0 | 11.337° | |
| 317 | 47128.310344520 | 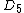 | 0 | 0 | 0 | 12 | 305 | 0 | 0 | 945 | 630 | 0 | 11.423° | |
| 318 | 47431.056020043 |  | 0 | 0 | 0 | 12 | 306 | 0 | 0 | 948 | 632 | 0 | 11.219° | |
| 334 | 52407.728127822 | 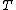 | 0 | 0 | 0 | 12 | 322 | 0 | 0 | 996 | 664 | 0 | 11.058° | |
| 348 | 56967.472454334 |  | 0 | 0 | 0 | 12 | 336 | 0 | 0 | 1038 | 692 | 0 | 10.721° | |
| 357 | 59999.922939598 | 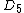 | 0 | 0 | 0 | 12 | 345 | 0 | 0 | 1065 | 710 | 0 | 10.728° | |
| 358 | 60341.830924588 | 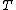 | 0 | 0 | 0 | 12 | 346 | 0 | 0 | 1068 | 712 | 0 | 10.647° | |
| 372 | 65230.027122557 |  | 0 | 0 | 0 | 12 | 360 | 0 | 0 | 1110 | 740 | 0 | 10.531° | |
| 382 | 68839.426839215 | 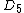 | 0 | 0 | 0 | 12 | 370 | 0 | 0 | 1140 | 760 | 0 | 10.379° | |
| 390 | 71797.035335953 |  | 0 | 0 | 0 | 12 | 378 | 0 | 0 | 1164 | 776 | 0 | 10.222° | |
| 392 | 72546.258370889 |  | 0 | 0 | 0 | 12 | 380 | 0 | 0 | 1170 | 780 | 0 | 10.278° | |
| 400 | 75582.448512213 | 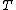 | 0 | 0 | 0 | 12 | 388 | 0 | 0 | 1194 | 796 | 0 | 10.068° | |
| 402 | 76351.192432673 | 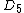 | 0 | 0 | 0 | 12 | 390 | 0 | 0 | 1200 | 800 | 0 | 10.099° | |
| 432 | 88353.709681956 |  | 0 | 0 | 0 | 24 | 396 | 12 | 0 | 1290 | 860 | 0 | 9.556° | |
| 448 | 95115.546986209 | 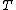 | 0 | 0 | 0 | 24 | 412 | 12 | 0 | 1338 | 892 | 0 | 9.322° | |
| 460 | 100351.763108673 | 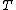 | 0 | 0 | 0 | 24 | 424 | 12 | 0 | 1374 | 916 | 0 | 9.297° | |
| 468 | 103920.871715127 | 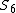 | 0 | 0 | 0 | 24 | 432 | 12 | 0 | 1398 | 932 | 0 | 9.120° | |
| 470 | 104822.886324279 | 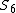 | 0 | 0 | 0 | 24 | 434 | 12 | 0 | 1404 | 936 | 0 | 9.059° |
According to a conjecture, if 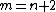 , p is the polyhedron formed by the convex hull of m points, q is the number of quadrilateral faces of p, then the solution for m electrons is f(m):
, p is the polyhedron formed by the convex hull of m points, q is the number of quadrilateral faces of p, then the solution for m electrons is f(m): 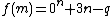 .[13]
.[13]
References
2. ^{{cite journal | first = S. | last = Smale |title = Mathematical Problems for the Next Century |journal = Mathematical Intelligencer |date =1998 |volume=20 |number=2 |pages=7–15|citeseerx = 10.1.1.35.4101 |doi=10.1007/bf03025291}}
3. ^{{cite journal|first1=L.|last1=Föppl |title=Stabile Anordnungen von Elektronen im Atom | journal = J. Reine Angew. Math. |number=141 |year=1912 |pages=251–301|url=http://eudml.org/doc/149380}}.
4. ^{{cite arXiv|last=Schwartz|first=Richard|eprint=1001.3702|title=The 5 electron case of Thomson's Problem|year=2010|class=math.MG}}
5. ^{{cite journal|first=V.A. |last=Yudin |title=The minimum of potential energy of a system of point charges |journal=Discretnaya Matematika |volume=4 |number=2|year=1992|pages= 115–121 (in Russian)}}; {{cite journal|first=V. A. |last=Yudin|journal= Discrete Math. Appl.|volume= 3 |number=1| year=1993|pages=75–81 |doi=10.1515/dma.1993.3.1.75 |title=The minimum of potential energy of a system of point charges}}
6. ^{{cite journal|first=N.N. |last= Andreev|title=An extremal property of the icosahedron| journal=East J. Approximation|volume=2 |number=4 |year=1996|pages=459–462}} {{MR|1426716}}, {{Zbl|0877.51021}}
7. ^Landkof, N. S. Foundations of modern potential theory. Translated from the Russian by A. P. Doohovskoy. Die Grundlehren der mathematischen Wissenschaften, Band 180. Springer-Verlag, New York-Heidelberg, 1972. x+424 pp.
8. ^Hardin, D. P.; Saff, E. B. Discretizing manifolds via minimum energy points. Notices Amer. Math. Soc. 51 (2004), no. 10, 1186–1194
9. ^Y. Levin and J. J. Arenzon, ``Why charges go to the Surface: A generalized Thomson Problem Europhys. Lett. Vol. 63 p. 415 (2003)
10. ^Sir J.J. Thomson, The Romanes Lecture, 1914 (The Atomic Theory)
11. ^{{cite journal|last=LaFave Jr|first=Tim|title=Correspondences between the classical electrostatic Thomson problem and atomic electronic structure|journal=Journal of Electrostatics|volume=71|issue=6|pages=1029–1035|date=December 2013|url=http://www.pagesofmind.com/FullTextPubs/La13-LaFave-2013-Correspondences-between-the-Thomson-Problem-and-Atomic-Structure.pdf|accessdate=10 Feb 2014|doi=10.1016/j.elstat.2013.10.001|arxiv=1403.2591|deadurl=yes|archiveurl=https://web.archive.org/web/20140222100807/http://www.pagesofmind.com/FullTextPubs/La13-LaFave-2013-Correspondences-between-the-Thomson-Problem-and-Atomic-Structure.pdf|archivedate=22 February 2014|df=}}
12. ^Kevin Brown."Min-Energy Configurations of Electrons On A Sphere".Retrieved 2014-05-01.
13. ^{{Cite web|url=https://oeis.org/A008486|title=Sloane's A008486 (see the comment from Feb 03 2017)|last=|first=|date=|website=The On-Line Encyclopedia of Integer Sequences|publisher=OEIS Foundation|access-date=2017-02-08}}
Notes
- {{cite journal|first1=L.L. |last1=Whyte|title=Unique arrangements of points on a sphere | journal = Amer. Math. Monthly |year=1952 |volume=59 | number=9 | pages=606–611|doi=10.2307/2306764|jstor=2306764}}
- {{cite journal|first1=Harvey |last1=Cohn|year=1956|title= Stability configurations of electrons on a sphere|journal=Math. Comput. |volume=10|issue=55| pages=117–120 | doi=10.1090/S0025-5718-1956-0081133-0 }}
- {{cite journal|first1=Michael | last1=Goldberg | title=Stability configurations of electrons on a sphere|journal=Math. Comp. | year=1969 | volume=23 | issue=108 | pages=785–786 | doi=10.1090/S0025-5718-69-99642-2 }}
- {{cite journal|first1=T. |last1=Erber|first2=G. M. |last2=Hockney | title= equilibrium configurations of N equal charges on a sphere|year=1991|journal=J. Phys. A: Math. Gen. |volume=24 | pages=L1369|doi=10.1088/0305-4470/24/23/008|number=23|bibcode=1991JPhA...24L1369E}}
- {{cite journal|first1=J. R. |last1=Morris|first2=D. M. |last2=Deaven|first3=K. M. | last3=Ho|title=Genetic-algorithm energy minimization for point charges on a sphere | journal = Phys. Rev. B |volume=53 |issue=4| year=1996|pages=R1740–R1743 |doi=10.1103/PhysRevB.53.R1740|bibcode=1996PhRvB..53.1740M|citeseerx=10.1.1.28.93}}
- {{cite book|first1=T.|last1= Erber |first2= G. M.|last2= Hockney|title=Complex Systems: Equilibrium Configurations of
 Equal Charges on a Sphere
Equal Charges on a Sphere  |journal= Advances in Chemical Physics|volume= 98|pages=495–594|year= 1997 |doi=10.1002/9780470141571.ch5|isbn= 9780470141571 }}.
|journal= Advances in Chemical Physics|volume= 98|pages=495–594|year= 1997 |doi=10.1002/9780470141571.ch5|isbn= 9780470141571 }}. - {{cite journal|first1=E. L. |last1=Altschuler | first2=T. J. |last2=Williams|first3=E. R. |last3=Ratner |first4=R. |last4=Tipton |first5=R. |last5=Stong |first6=F. |last6=Dowla | first7=F. | last7=Wooten|title=Possible global minimum lattice configurations for Thomson's problem of charges on a sphere|year=1997|journal = Phys. Rev. Lett. |volume=78 |issue=14 | pages=2681–2685 |doi=10.1103/PhysRevLett.78.2681|bibcode=1997PhRvL..78.2681A }}
- {{cite journal|first1=M. |last1=Bowick|first2=A. | last2=Cacciuto|first3=D. R. | last3=Nelson|first4=A. | last4=Travesset |title=Crystalline order on a sphere and the generalized Thomson Problem|journal=Phys. Rev. Lett. | volume= 89 |year=2002 |pages=249902 | doi=10.1103/PhysRevLett.89.185502|pmid=12398614| issue=18|arxiv=cond-mat/0206144|bibcode=2002PhRvL..89r5502B}}
- {{cite journal|first1=P. D.|last1= Dragnev|first2= D. A.|last2= Legg|first3= D. W. |last3= Townsend |title=Discrete logarithmic energy on the sphere|journal=Pacific J. Math. |volume=207 |year=2002|number= 2|pages= 345–358|doi=10.2140/pjm.2002.207.345}}.
- {{cite journal|first1=A. | last1=Katanforoush |first2=M. |last2=Shahshahani | title=Distributing points on the sphere. I|year=2003 | journal=Exper. Math. |volume=12|number=2| pages=199–209 |doi=10.1080/10586458.2003.10504492}}
- {{cite journal|first1=David J. | last1=Wales |first2=Sidika|last2=Ulker| title=Structure and dynamics of spherical crystals characterized for the Thomson problem | journal=Phys. Rev. B | volume=74 | year=2006|number=21|pages=212101 |doi=10.1103/PhysRevB.74.212101|bibcode=2006PhRvB..74u2101W}} Configurations reprinted in {{cite web | first1=D. J. | last1=Wales | first2=S. | last2=Ulker | url=http://www-wales.ch.cam.ac.uk/~wales/CCD/Thomson/table.html|title=The Cambridge cluster database}}
- {{cite journal|first1=A. |last1=Slosar|first2=R. | last2=Podgornik|title= On the connected-charges Thomson problem|journal=Europhys. Lett.|year=2006|volume=75|number=4|pages=631|doi=10.1209/epl/i2006-10146-1|arxiv=cond-mat/0606765|bibcode=2006EL.....75..631S}}
- {{cite journal|first1=Henry |last1= Cohn |first2= Abhinav|last2= Kumar |title=Universally optimal distribution of points on spheres|journal=J. Amer. Math. Soc. |volume= 20 |year=2007|number= 1|pages=99–148 |doi=10.1090/S0894-0347-06-00546-7|arxiv=math/0607446|bibcode=2007JAMS...20...99C}}
- {{cite journal|first1=D. J. | last1=Wales|first2=H. | last2=McKay | first3=E. L. | last3=Altschuler| title=Defect motifs for spherical topologies| journal=Phys. Rev. B|year=2009 | volume=79 | pages=224115 | issue=22 | doi=10.1103/PhysRevB.79.224115| bibcode=2009PhRvB..79v4115W}}. Configurations reproduced in {{cite web|first1=D. J. | last1=Wales | first2=S. | last2=Ulker | url=http://www-wales.ch.cam.ac.uk/~wales/CCD/Thomson2/table.html|title=The Cambridge cluster database}}
- {{cite journal|first1=W. J. M. |last1=Ridgway |first2=A. F. | last2=Cheviakov|doi=10.1016/j.cpc.2018.03.029| year=2018|journal=Comput. Phys. Commun. | title=An iterative procedure for finding locally and globally optimal arrangements of particles on the unit sphere|volume=233|pages=84–109}}
- {{cite web|first1=Cris|last1= Cecka|first2= Mark J. |last2= Bowick|first3= Alan A.|last3= Middleton|url= http://thomson.phy.syr.edu/|title= Thomson Problem @ S.U.}}
- J. C. L. Gieseler
- J. Clifford Hudson
- J. Clin. Invest.
- J.C. Lodge
- J. C. Love Field
- J. C. Love Field at Pat Patterson Park
- JCLU
- J.C. MacKenzie
- JC Mackenzie
- J. C. Mackenzie
- J. C. MacKenzie
- J.C. Mackenzie
- J.C. Mahindra
- J. C. Mangan
- J. C. Martin
- J.C. Martin
- JCMateri
- J.C. Mayfield
- JCMC
- J. C. McDonald
- J.C. McDonald
- JC Midge
- Jc midge
- JCMidge
- J.C. Molland