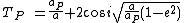- Definition
- Applications
- Related notions
- See also
- References
- External links
Tisserand's parameter (or Tisserand's invariant) is a value calculated from several orbital elements (semi-major axis, orbital eccentricity and inclination) of a relatively small object and a larger "perturbing body". It is used to distinguish different kinds of orbits. The term is named after French astronomer Félix Tisserand, and applies to restricted three-body problems in which the three objects all differ greatly in mass.
Definition
For a small body with semi-major axis 
, eccentricity 
, and inclination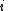 
, relative to the orbit of a perturbing larger body with semimajor axis 
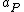, the parameter is defined as follows:[1]
The quasi-conservation of Tisserand's parameter is a consequence of Tisserand's relation.
Applications
- TJ, Tisserand's parameter with respect to Jupiter as perturbing body, is frequently used to distinguish asteroids (typically
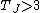) from Jupiter-family comets (typically 
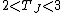).[2] - The minor planet group of damocloids are defined by a Jupiter Tisserand's parameter of 2 or less ({{math|TJ ≤ 2}}).
- The roughly constant value of the parameter before and after the interaction (encounter) is used to determine whether or not an observed orbiting body is the same as one previously observed in Tisserand's criterion.
- The quasi-conservation of Tisserand's parameter constrains the orbits attainable using gravity assist for outer Solar System exploration.
- TN, Tisserand's parameter with respect to Neptune, has been suggested to distinguish near-scattered (affected by Neptune) from extended-scattered trans-Neptunian objects (not affected by Neptune; e.g. 90377 Sedna).
- Tisserand's parameter could be used to infer the presence of an intermediate-mass black hole at the center of the Milky Way using the motions of orbiting stars.[3]
Related notions
The parameter is derived from one of the so-called Delaunay standard variables, used to study the perturbed Hamiltonian in a three-body system. Ignoring higher-order perturbation terms, the following value is conserved:
Consequently, perturbations may lead to the resonance between the orbital inclination and eccentricity, known as Kozai resonance. Near-circular, highly inclined orbits can thus become very eccentric in exchange for lower inclination. For example, such a mechanism can produce sungrazing comets, because a large eccentricity with a constant semimajor axis results in a small perihelion.
See also
- Tisserand's relation for the derivation and the detailed assumptions
References
2. ^{{Cite web|url=http://www2.ess.ucla.edu/~jewitt/tisserand.html|title=Dave Jewitt: Tisserand Parameter|website=www2.ess.ucla.edu|access-date=2018-03-27}}
3. ^{{cite book|last=Merritt|first=David|title=Dynamics and Evolution of Galactic Nuclei|year=2013|publisher=Princeton University Press|location=Princeton, NJ|isbn=9781400846122|url=https://openlibrary.org/works/OL16802359W/Dynamics_and_Evolution_of_Galactic_Nuclei}}
}}
External links
- David Jewitt's page on Tisserand's parameter
- [https://farside.ph.utexas.edu/teaching/336k/Newtonhtml/node122.html Tisserand criterion]
- Evgenij Miroshnichenko
- Evgeni Karpoukhine
- Evgeni Kets
- Evgeni Kirilov
- Evgeniko
- Evgeniko, Greece
- Evgenikon
- Evgenikon, Greece
- Evgeni Krasnopolski
- Evgenikó
- Evgenikó, Greece
- Evgenikón
- Evgenikón, Greece
- Evgeni Leonov
- Evgeni Malkin
- Evgeni Mikeladze
- Evgeni Miller
- Evgeni Morgunov
- Evgeni nabakov
- Evgeni Onegin
- Evgeni Paladiev
- Evgeni Petrov (cyclist)
- Evgeni Platov
- Evgeni Pleschenko
- Evgeni Pleshenko