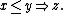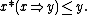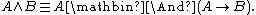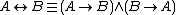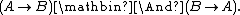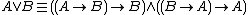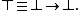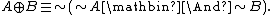请输入您要查询的百科知识：

　

词条 T-norm fuzzy logics
释义

  1. Motivation

  2. History

  3. Logical language

  4. Semantics

  5. Bibliography

  6. References

T-norm fuzzy logics are a family of non-classical logics, informally delimited by having a semantics that takes the real unit interval [0, 1] for the system of truth values and functions called t-norms for permissible interpretations of conjunction. They are mainly used in applied fuzzy logic and fuzzy set theory as a theoretical basis for approximate reasoning.

T-norm fuzzy logics belong in broader classes of fuzzy logics and many-valued logics. In order to generate a well-behaved implication, the t-norms are usually required to be left-continuous; logics of left-continuous t-norms further belong in the class of substructural logics, among which they are marked with the validity of the law of prelinearity, (A → B) ∨ (B → A). Both propositional and first-order (or higher-order) t-norm fuzzy logics, as well as their expansions by modal and other operators, are studied. Logics that restrict the t-norm semantics to a subset of the real unit interval (for example, finitely valued Łukasiewicz logics) are usually included in the class as well.

Important examples of t-norm fuzzy logics are monoidal t-norm logic MTL of all left-continuous t-norms, basic logic BL of all continuous t-norms, product fuzzy logic of the product t-norm, or the nilpotent minimum logic of the nilpotent minimum t-norm. Some independently motivated logics belong among t-norm fuzzy logics, too, for example Łukasiewicz logic (which is the logic of the Łukasiewicz t-norm) or Gödel–Dummett logic (which is the logic of the minimum t-norm).

Motivation

As members of the family of fuzzy logics, t-norm fuzzy logics primarily aim at generalizing classical two-valued logic by admitting intermediary truth values between 1 (truth) and 0 (falsity) representing degrees of truth of propositions. The degrees are assumed to be real numbers from the unit interval [0, 1]. In propositional t-norm fuzzy logics, propositional connectives are stipulated to be truth-functional, that is, the truth value of a complex proposition formed by a propositional connective from some constituent propositions is a function (called the truth function of the connective) of the truth values of the constituent propositions. The truth functions operate on the set of truth degrees (in the standard semantics, on the [0, 1] interval); thus the truth function of an n-ary propositional connective c is a function Fc: [0, 1]n → [0, 1]. Truth functions generalize truth tables of propositional connectives known from classical logic to operate on the larger system of truth values.

T-norm fuzzy logics impose certain natural constraints on the truth function of conjunction. The truth function 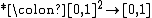of conjunction is assumed to satisfy the following conditions:

  • Commutativity, that is, 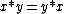for all x and y in [0, 1]. This expresses the assumption that the order of fuzzy propositions is immaterial in conjunction, even if intermediary truth degrees are admitted.
  • Associativity, that is, 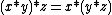for all x, y, and z in [0, 1]. This expresses the assumption that the order of performing conjunction is immaterial, even if intermediary truth degrees are admitted.
  • Monotony, that is, if then 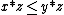for all x, y, and z in [0, 1]. This expresses the assumption that increasing the truth degree of a conjunct should not decrease the truth degree of the conjunction.
  • Neutrality of 1, that is, 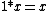for all x in [0, 1]. This assumption corresponds to regarding the truth degree 1 as full truth, conjunction with which does not decrease the truth value of the other conjunct. Together with the previous conditions this condition ensures that also for all x in [0, 1], which corresponds to regarding the truth degree 0 as full falsity, conjunction with which is always fully false.
  • Continuity of the function (the previous conditions reduce this requirement to the continuity in either argument). Informally this expresses the assumption that microscopic changes of the truth degrees of conjuncts should not result in a macroscopic change of the truth degree of their conjunction. This condition, among other things, ensures a good behavior of (residual) implication derived from conjunction; to ensure the good behavior, however, left-continuity (in either argument) of the function is sufficient.[1] In general t-norm fuzzy logics, therefore, only left-continuity of is required, which expresses the assumption that a microscopic decrease of the truth degree of a conjunct should not macroscopically decrease the truth degree of conjunction.

These assumptions make the truth function of conjunction a left-continuous t-norm, which explains the name of the family of fuzzy logics (t-norm based). Particular logics of the family can make further assumptions about the behavior of conjunction (for example, Gödel logic requires its idempotence) or other connectives (for example, the logic IMTL requires the involutiveness of negation).

All left-continuous t-norms have a unique residuum, that is, a binary function such that for all x, y, and z in [0, 1],

if and only if

The residuum of a left-continuous t-norm can explicitly be defined as

This ensures that the residuum is the pointwise largest function such that for all x and y,

The latter can be interpreted as a fuzzy version of the modus ponens rule of inference. The residuum of a left-continuous t-norm thus can be characterized as the weakest function that makes the fuzzy modus ponens valid, which makes it a suitable truth function for implication in fuzzy logic. Left-continuity of the t-norm is the necessary and sufficient condition for this relationship between a t-norm conjunction and its residual implication to hold.

Truth functions of further propositional connectives can be defined by means of the t-norm and its residuum, for instance the residual negation or bi-residual equivalence Truth functions of propositional connectives may also be introduced by additional definitions: the most usual ones are the minimum (which plays a role of another conjunctive connective), the maximum (which plays a role of a disjunctive connective), or the Baaz Delta operator, defined in [0, 1] as 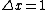if and otherwise. In this way, a left-continuous t-norm, its residuum, and the truth functions of additional propositional connectives determine the truth values of complex propositional formulae in [0, 1].

Formulae that always evaluate to 1 are called tautologies with respect to the given left-continuous t-norm 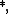or tautologies. The set of all tautologies is called the logic of the t-norm 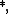as these formulae represent the laws of fuzzy logic (determined by the t-norm) which hold (to degree 1) regardless of the truth degrees of atomic formulae. Some formulae are tautologies with respect to a larger class of left-continuous t-norms; the set of such formulae is called the logic of the class. Important t-norm logics are the logics of particular t-norms or classes of t-norms, for example:

  • Łukasiewicz logic is the logic of the Łukasiewicz t-norm
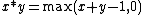
  • Gödel–Dummett logic is the logic of the minimum t-norm
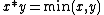
  • Product fuzzy logic is the logic of the product t-norm
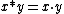
  • Monoidal t-norm logic MTL is the logic of (the class of) all left-continuous t-norms
  • Basic fuzzy logic BL is the logic of (the class of) all continuous t-norms

It turns out that many logics of particular t-norms and classes of t-norms are axiomatizable. The completeness theorem of the axiomatic system with respect to the corresponding t-norm semantics on [0, 1] is then called the standard completeness of the logic. Besides the standard real-valued semantics on [0, 1], the logics are sound and complete with respect to general algebraic semantics, formed by suitable classes of prelinear commutative bounded integral residuated lattices.

History

Some particular t-norm fuzzy logics have been introduced and investigated long before the family was recognized (even before the notions of fuzzy logic or t-norm emerged):

  • Łukasiewicz logic (the logic of the Łukasiewicz t-norm) was originally defined by Jan Łukasiewicz (1920) as a three-valued logic;[2] it was later generalized to n-valued (for all finite n) as well as infinitely-many-valued variants, both propositional and first-order.[3]
  • Gödel–Dummett logic (the logic of the minimum t-norm) was implicit in Gödel's 1932 proof of infinite-valuedness of intuitionistic logic.[4] Later (1959) it was explicitly studied by Dummett who proved a completeness theorem for the logic.[5]

A systematic study of particular t-norm fuzzy logics and their classes began with Hájek's (1998) monograph Metamathematics of Fuzzy Logic, which presented the notion of the logic of a continuous t-norm, the logics of the three basic continuous t-norms (Łukasiewicz, Gödel, and product), and the 'basic' fuzzy logic BL of all continuous t-norms (all of them both propositional and first-order). The book also started the investigation of fuzzy logics as non-classical logics with Hilbert-style calculi, algebraic semantics, and metamathematical properties known from other logics (completeness theorems, deduction theorems, complexity, etc.).

Since then, a plethora of t-norm fuzzy logics have been introduced and their metamathematical properties have been investigated. Some of the most important t-norm fuzzy logics were introduced in 2001, by Esteva and Godo (MTL, IMTL, SMTL, NM, WNM),[1] Esteva, Godo, and Montagna (propositional ŁΠ),[6] and Cintula (first-order ŁΠ).[7]

Logical language

The logical vocabulary of propositional t-norm fuzzy logics standardly comprises the following connectives:

  • Implication (binary). In the context of other than t-norm-based fuzzy logics, the t-norm-based implication is sometimes called residual implication or R-implication, as its standard semantics is the residuum of the t-norm that realizes strong conjunction.
  • Strong conjunction 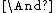(binary). In the context of substructural logics, the sign and the names group, intensional, multiplicative, or parallel conjunction are often used for strong conjunction.
  • Weak conjunction (binary), also called lattice conjunction (as it is always realized by the lattice operation of meet in algebraic semantics). In the context of substructural logics, the names additive, extensional, or comparative conjunction are sometimes used for lattice conjunction. In the logic BL and its extensions (though not in t-norm logics in general), weak conjunction is definable in terms of implication and strong conjunction, by

The presence of two conjunction connectives is a common feature of contraction-free substructural logics.

  • Bottom (nullary); or are common alternative signs and zero a common alternative name for the propositional constant (as the constants bottom and zero of substructural logics coincide in t-norm fuzzy logics). The proposition represents the falsity or absurdum and corresponds to the classical truth value false.
  • Negation (unary), sometimes called residual negation if other negation connectives are considered, as it is defined from the residual implication by the reductio ad absurdum:

  • Equivalence (binary), defined as

In t-norm logics, the definition is equivalent to

  • (Weak) disjunction (binary), also called lattice disjunction (as it is always realized by the lattice operation of join in algebraic semantics). In t-norm logics it is definable in terms of other connectives as

  • Top 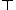(nullary), also called one and denoted by or 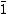(as the constants top and zero of substructural logics coincide in t-norm fuzzy logics). The proposition 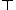corresponds to the classical truth value true and can in t-norm logics be defined as

Some propositional t-norm logics add further propositional connectives to the above language, most often the following ones:

  • The Delta connective is a unary connective that asserts classical truth of a proposition, as the formulae of the form behave as in classical logic. Also called the Baaz Delta, as it was first used by Matthias Baaz for Gödel–Dummett logic.[8] The expansion of a t-norm logic by the Delta connective is usually denoted by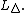
  • Truth constants are nullary connectives representing particular truth values between 0 and 1 in the standard real-valued semantics. For the real number , the corresponding truth constant is usually denoted by 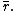Most often, the truth constants for all rational numbers are added. The system of all truth constants in the language is supposed to satisfy the bookkeeping axioms:[9]

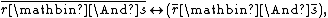
etc. for all propositional connectives and all truth constants definable in the language.

  • Involutive negation (unary) can be added as an additional negation to t-norm logics whose residual negation is not itself involutive, that is, if it does not obey the law of double negation 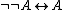. A t-norm logic expanded with involutive negation is usually denoted by 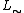and called with involution.
  • Strong disjunction (binary). In the context of substructural logics it is also called group, intensional, multiplicative, or parallel disjunction. Even though standard in contraction-free substructural logics, in t-norm fuzzy logics it is usually used only in the presence of involutive negation, which makes it definable (and so axiomatizable) by de Morgan's law from strong conjunction:

  • Additional t-norm conjunctions and residual implications. Some expressively strong t-norm logics, for instance the logic ŁΠ, have more than one strong conjunction or residual implication in their language. In the standard real-valued semantics, all such strong conjunctions are realized by different t-norms and the residual implications by their residua.

Well-formed formulae of propositional t-norm logics are defined from propositional variables (usually countably many) by the above logical connectives, as usual in propositional logics. In order to save parentheses, it is common to use the following order of precedence:

  • Unary connectives (bind most closely)
  • Binary connectives other than implication and equivalence
  • Implication and equivalence (bind most loosely)

First-order variants of t-norm logics employ the usual logical language of first-order logic with the above propositional connectives and the following quantifiers:

  • General quantifier
  • Existential quantifier

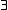
The first-order variant of a propositional t-norm logic is usually denoted by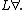

Semantics

Algebraic semantics is predominantly used for propositional t-norm fuzzy logics, with three main classes of algebras with respect to which a t-norm fuzzy logic is complete:

  • General semantics, formed of all -algebras — that is, all algebras for which the logic is sound.
  • Linear semantics, formed of all linear -algebras — that is, all -algebras whose lattice order is linear.
  • Standard semantics, formed of all standard -algebras — that is, all -algebras whose lattice reduct is the real unit interval [0, 1] with the usual order. In standard -algebras, the interpretation of strong conjunction is a left-continuous t-norm and the interpretation of most propositional connectives is determined by the t-norm (hence the names t-norm-based logics and t-norm -algebras, which is also used for -algebras on the lattice [0, 1]). In t-norm logics with additional connectives, however, the real-valued interpretation of the additional connectives may be restricted by further conditions for the t-norm algebra to be called standard: for example, in standard 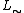-algebras of the logic with involution, the interpretation of the additional involutive negation is required to be the standard involution 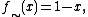rather than other involutions which can also interpret over t-norm 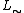-algebras.[10] In general, therefore, the definition of standard t-norm algebras has to be explicitly given for t-norm logics with additional connectives.

Bibliography

  • Esteva F. & Godo L., 2001, "Monoidal t-norm based logic: Towards a logic of left-continuous t-norms". Fuzzy Sets and Systems 124: 271–288.
  • Flaminio T. & Marchioni E., 2006, T-norm based logics with an independent involutive negation. Fuzzy Sets and Systems 157: 3125–3144.
  • Gottwald S. & Hájek P., 2005, Triangular norm based mathematical fuzzy logic. In E.P. Klement & R. Mesiar (eds.), Logical, Algebraic, Analytic and Probabilistic Aspects of Triangular Norms, pp. 275–300. Elsevier, Amsterdam 2005.
  • Hájek P., 1998, Metamathematics of Fuzzy Logic. Dordrecht: Kluwer. {{isbn|0-7923-5238-6}}.

References

1. ^1 Esteva & Godo (2001)
2. ^Łukasiewicz J., 1920, O logice trojwartosciowej (Polish, On three-valued logic). Ruch filozoficzny 5:170–171.
3. ^Hay, L.S., 1963, Axiomatization of the infinite-valued predicate calculus. Journal of Symbolic Logic 28:77–86.
4. ^Gödel K., 1932, Zum intuitionistischen Aussagenkalkül, Anzeiger Akademie der Wissenschaften Wien 69: 65–66.
5. ^Dummett M., 1959, Propositional calculus with denumerable matrix, Journal of Symbolic Logic 27: 97–106
6. ^Esteva F., Godo L., & Montagna F., 2001, The ŁΠ and ŁΠ½ logics: Two complete fuzzy systems joining Łukasiewicz and product logics, Archive for Mathematical Logic 40: 39–67.
7. ^Cintula P., 2001, The ŁΠ and ŁΠ½ propositional and predicate logics, Fuzzy Sets and Systems 124: 289–302.
8. ^Baaz M., 1996, Infinite-valued Gödel logic with 0-1-projections and relativisations. In P. Hájek (ed.), Gödel'96: Logical Foundations of Mathematics, Computer Science, and Physics, Springer, Lecture Notes in Logic 6: 23–33
9. ^Hájek (1998)
10. ^Flaminio & Marchioni (2006)

1 : Fuzzy logic
随便看

　

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。

　

Copyright © 2023 OENC.NET All Rights Reserved
京ICP备2021023879号 更新时间：2024/11/11 12:15:05