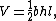- As a semiregular (or uniform) polyhedron
- Volume
- Truncated triangular prism
- Facetings
- Related polyhedra and tilings Symmetry mutations Compounds Honeycombs Related polytopes Four dimensional space
- See also
- References
In geometry, a triangular prism is a three-sided prism; it is a polyhedron made of a triangular base, a translated copy, and 3 faces joining corresponding sides. A right triangular prism has rectangular sides, otherwise it is oblique. A uniform triangular prism is a right triangular prism with equilateral bases, and square sides.
Equivalently, it is a polyhedron of which two faces are parallel, while the surface normals of the other three are in the same plane (which is not necessarily parallel to the base planes). These three faces are parallelograms. All cross-sections parallel to the base faces are the same triangle.
As a semiregular (or uniform) polyhedron
A right triangular prism is semiregular or, more generally, a uniform polyhedron if the base faces are equilateral triangles, and the other three faces are squares. It can be seen as a truncated trigonal hosohedron, represented by Schläfli symbol t{2,3}. Alternately it can be seen as the Cartesian product of a triangle and a line segment, and represented by the product {3}x{}. The dual of a triangular prism is a triangular bipyramid.
The symmetry group of a right 3-sided prism with triangular base is D3h of order 12. The rotation group is D3 of order 6. The symmetry group does not contain inversion.
Volume
The volume of any prism is the product of the area of the base and the distance between the two bases. In this case the base is a triangle so we simply need to compute the area of the triangle and multiply this by the length of the prism:
where {{mvar|b}} is the length of one side of the triangle, {{mvar|h}} is the length of an altitude drawn to that side, and {{mvar|l}} is the distance between the triangular faces.
Truncated triangular prism
A truncated right triangular prism has one triangular face truncated (planed) at an oblique angle.[1]
Facetings
There are two full D2h symmetry facetings of a triangular prism, both with 6 isosceles triangle faces, one keeping the original top and bottom triangles, and one the original squares. Two lower C3v symmetry faceting have one base triangle, 3 lateral crossed square faces, and 3 isosceles triangle lateral faces.
| Convex | Facetings | |||
|---|---|---|---|---|
| D3h symmetry | C3v symmetry | |||
| 2 {3} 3 {4} | 3 {4} 6 ( ) v { } | 2 {3} 6 ( ) v { } | 1 {3} 3 t'{2} 6 ( ) v { } | 1 {3} 3 t'{2} 3 ( ) v { } |
Related polyhedra and tilings
{{UniformPrisms}}{{Cupolae}}Symmetry mutations
This polyhedron is topologically related as a part of sequence of uniform truncated polyhedra with vertex configurations (3.2n.2n), and [n,3] Coxeter group symmetry.
{{Truncated figure1 table}}This polyhedron is topologically related as a part of sequence of cantellated polyhedra with vertex figure (3.4.n.4), and continues as tilings of the hyperbolic plane. These vertex-transitive figures have (*n32) reflectional symmetry.
This polyhedron is topologically related as a part of sequence of cantellated polyhedra with vertex figure (3.4.n.4), and continues as tilings of the hyperbolic plane. These vertex-transitive figures have (*n32) reflectional symmetry.
{{Expanded small table}}Compounds
There are 4 uniform compounds of triangular prisms:
Compound of four triangular prisms, compound of eight triangular prisms, compound of ten triangular prisms, compound of twenty triangular prisms.
Honeycombs
There are 9 uniform honeycombs that include triangular prism cells:
Gyroelongated alternated cubic honeycomb, elongated alternated cubic honeycomb, gyrated triangular prismatic honeycomb, snub square prismatic honeycomb, triangular prismatic honeycomb, triangular-hexagonal prismatic honeycomb, truncated hexagonal prismatic honeycomb, rhombitriangular-hexagonal prismatic honeycomb, snub triangular-hexagonal prismatic honeycomb, elongated triangular prismatic honeycomb
Related polytopes
The triangular prism is first in a dimensional series of semiregular polytopes. Each progressive uniform polytope is constructed vertex figure of the previous polytope. Thorold Gosset identified this series in 1900 as containing all regular polytope facets, containing all simplexes and orthoplexes (equilateral triangles and squares in the case of the triangular prism). In Coxeter's notation the triangular prism is given the symbol −121.
{{Gosset_semiregular_polytopes}}Four dimensional space
The triangular prism exists as cells of a number of four-dimensional uniform 4-polytopes, including:
| Four dimensional polytopes with triangular prisms | |||||||
|---|---|---|---|---|---|---|---|
| {{CDD>node_1|3|node|3|node|2|node_1}} | {{CDD>node_1|3|node|4|node|2|node_1}} | {{CDD>node|3|node_1|4|node|2|node_1}} | {{CDD>node_1|3|node|5|node|2|node_1}} | {{CDD>node|3|node_1|5|node|2|node_1}} | {{CDD>node|3|node_1|5|node_1|2|node_1}} | ||
| {{CDD>node_1|3|node|5|node_1|2|node_1}} | {{CDD>node_1|3|node|4|node_1|2|node_1}} | {{CDD>node|3|node_1|4|node_1|2|node_1}} | {{CDD>node_h|5|node_h|3|node_h|2|node_1}} | {{CDD>node_h|n|node_h|2x|node_h|2|node_1}} | |||
| {{CDD>node_1|3|node|3|node_1|3|node}} | {{CDD>node_1|3|node_1|3|node_1|3|node}} | {{CDD>node_1|3|node|3|node|3|node_1}} | {{CDD>node_1|3|node_1|3|node|3|node_1}} | {{CDD>node_1|4|node|3|node_1|3|node}} | {{CDD>node_1|4|node_1|3|node_1|3|node}} | {{CDD>node_1|4|node|3|node|3|node_1}} | {{CDD>node_1|4|node_1|3|node|3|node_1}} |
| {{CDD>node_1|3|node|4|node_1|3|node}} | {{CDD>node_1|3|node_1|4|node_1|3|node}} | {{CDD>node_1|3|node|4|node|3|node_1}} | {{CDD>node_1|3|node_1|4|node|3|node_1}} | {{CDD>node_1|5|node|3|node_1|3|node}} | {{CDD>node_1|5|node_1|3|node_1|3|node}} | {{CDD>node_1|5|node|3|node|3|node_1}} | {{CDD>node_1|5|node_1|3|node|3|node_1}} |
See also
- Wedge (geometry)
References
- {{mathworld | urlname = TriangularPrism | title = Triangular prism}}
- [https://web.archive.org/web/20150417184747/http://polyhedra.org/poly/show/22/triangular_prism Interactive Polyhedron: Triangular Prism]
- surface area and volume of a triangular prism
- Janker (disambiguation)
- Jan Khani
- Jan Khatun
- Jankhilavan Jasoos
- Jankho Huyo
- Jankho Karka
- Jankho Khala
- Jankho Khalani
- Jankho Kharka
- Jankho Khota
- Jankho Kkollu
- Jankho Kkota
- Jankho Kota
- Jankia
- Jankibai
- Jankidas Mehra
- Janki Devi Memorial College
- Jan Kinder
- Jan Kip and Leonard Knyff
- Janki Vallabh
- Jan Kjaerulff
- Jan Kjellvander
- Jan Kjærulff
- Jan Klabbers
- Jan Klapac