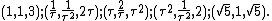“Truncated dodecadodecahedron”的意思、由来-开放百科全书

In geometry, the truncated dodecadodecahedron is a nonconvex uniform polyhedron, indexed as U₅₉. It is given a Schläfli symbol t_0,1,2{5/3,5}. It has 120 vertices and 54 faces: 30 squares, 12 decagons, and 12 decagrams. The central region of the polyhedron is connected to the exterior via 20 small triangular holes.

The name truncated dodecadodecahedron is somewhat misleading: truncation of the dodecadodecahedron would produce rectangular faces rather than squares, and the pentagram faces of the dodecahedron would turn into truncated pentagrams rather than decagrams. However, it is the quasitruncation of the dodecadodecahedron, as defined by {{harvtxt|Coxeter|Longuet-Higgins|Miller|1954}}.^[1] For this reason, it is also known as the quasitruncated dodecadodecahedron.^[2] Coxeter et al. credit its discovery to a paper published in 1881 by Austrian mathematician Johann Pitsch.^[3]

Cartesian coordinates

Cartesian coordinates for the vertices of a truncated dodecadodecahedron are all the triples of numbers obtained by circular shifts and sign changes from the following points (where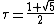

is the golden ratio):

Each of these five points has eight possible sign patterns and three possible circular shifts, giving a total of 120 different points.

As a Cayley graph

The truncated dodecadodecahedron forms a Cayley graph for the symmetric group on five elements, as generated by two group members: one that swaps the first two elements of a five-tuple, and one that performs a circular shift operation on the last four elements. That is, the 120 vertices of the polyhedron may be placed in one-to-one correspondence with the 5! permutations on five elements, in such a way that the three neighbors of each vertex are the three permutations formed from it by swapping the first two elements or circularly shifting (in either direction) the last four elements.^[4]

Related polyhedra

Medial disdyakis triacontahedron

The medial disdyakis triacontahedron is a nonconvex isohedral polyhedron. It is the dual of the uniform truncated dodecadodecahedron.

See also

References

1. ^{{citation | last1 = Coxeter | first1 = H. S. M. | author1-link = Harold Scott MacDonald Coxeter | last2 = Longuet-Higgins | first2 = M. S. | author2-link = Michael S. Longuet-Higgins | last3 = Miller | first3 = J. C. P. | author3-link = J. C. P. Miller | journal = Philosophical Transactions of the Royal Society of London. Series A. Mathematical and Physical Sciences | jstor = 91532 | mr = 0062446 | pages = 401–450 | title = Uniform polyhedra | volume = 246 | year = 1954 | doi=10.1098/rsta.1954.0003| bibcode = 1954RSPTA.246..401C}}. See especially the description as a quasitruncation on p. 411 and the photograph of a model of its skeleton in Fig. 114, Plate IV.
2. ^Wenninger writes "quasitruncated dodecahedron", but this appear to be a mistake. {{citation|contribution=98 Quasitruncated dodecahedron|pages=152–153|first=Magnus J.|last=Wenninger|authorlink=Magnus Wenninger|title=Polyhedron Models|publisher=Cambridge University Press|year=1971}}.
3. ^{{citation | last = Pitsch | first = Johann | journal = Zeitschrift für das Realschulwesen | pages = 9–24, 72–89, 216 | title = Über halbreguläre Sternpolyeder | volume = 6 | year = 1881}}. According to {{harvtxt|Coxeter|Longuet-Higgins|Miller|1954}}, the truncated dodecadodecahedron appears as no. XII on p.86.
4. ^{{citation | last = Eppstein | first = David | authorlink = David Eppstein | editor1-last = Tollis | editor1-first = Ioannis G. | editor2-last = Patrignani | editor2-first = Marizio | arxiv = 0709.4087 | contribution = The topology of bendless three-dimensional orthogonal graph drawing | doi = 10.1007/978-3-642-00219-9_9 | location = Heraklion, Crete | pages = 78–89 | publisher = Springer-Verlag | series = Lecture Notes in Computer Science | title = Proc. 16th Int. Symp. Graph Drawing | volume = 5417 | year = 2008}}.

Cartesian coordinates

As a Cayley graph

Related polyhedra

Medial disdyakis triacontahedron

See also

References

External links