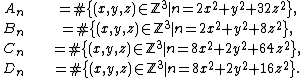- Congruent number problem
- Theorem
- History
- Importance
- See also
- References
In number theory, Tunnell's theorem gives a partial resolution to the congruent number problem, and under the Birch and Swinnerton-Dyer conjecture, a full resolution.
Congruent number problem
{{main|Congruent number problem}}The congruent number problem asks which positive integers can be the area of a right triangle with all three sides rational. Tunnell's theorem relates this to the number of integral solutions of a few fairly simple Diophantine equations.
Theorem
For a given square-free integer n, define
Tunnell's theorem states that supposing n is a congruent number, if n is odd then 2An = Bn and if n is even then 2Cn = Dn. Conversely, if the Birch and Swinnerton-Dyer conjecture holds true for elliptic curves of the form 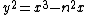 , these equalities are sufficient to conclude that n is a congruent number.
, these equalities are sufficient to conclude that n is a congruent number.
History
The theorem is named for Jerrold B. Tunnell, a number theorist at Rutgers University, who proved it in {{Harvtxt|Tunnell|1983}}.
Importance
The importance of Tunnell's theorem is that the criterion it gives is testable by a finite calculation. For instance, for a given n, the numbers An,Bn,Cn,Dn can be calculated by exhaustively searching through x,y,z in the range 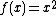 .
.
See also
{{Div col}}- Birch and Swinnerton-Dyer conjecture
- Congruent number
References
- {{citation
| last = Koblitz
| first = Neal
| authorlink = Neal Koblitz
| title = Introduction to Elliptic Curves and Modular Forms
| edition = 2nd
| series = Graduate Texts in Mathematics (Book 97)
| publisher = Springer-Verlag
| year = 2012
| isbn = 978-1-4612-6942-7}}
- {{citation
| last = Tunnell
| first = Jerrold B.
| authorlink = Jerrold B. Tunnell
| title = A classical Diophantine problem and modular forms of weight 3/2
| journal = Inventiones Mathematicae
| volume = 72
| issue = 2
| pages = 323–334
| year = 1983
| doi = 10.1007/BF01389327
| url = http://www.digizeitschriften.de/dms/img/?PID=GDZPPN002099403}}
- Mocheni
- Mocheno language
- Mochiaki Hachisuka
- Mochibun kaisha
- Mochica Culture
- Mochi Craft
- Mochi crunch
- Mochi Darwaza
- Mochida Station
- Mochi (disambiguation)
- Mochi (food)
- Mochi Gate
- Mochi ice
- Mochi ice cream
- Mochi (Japanese)
- Mochika
- Mochika language
- Mochikit
- MochiKit
- Mochikyūkin
- Mochima National Park
- MOCHIP
- Mochi Pura
- Mochitsura Hashimoto
- Mochiuji Ashikaga