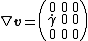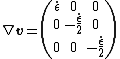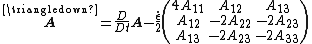1. Examples for the symmetric tensor A
    Simple shear  Uniaxial extension of incompressible fluid 

2. See also

3. References

In continuum mechanics, including fluid dynamics, an upper-convected time derivative or Oldroyd derivative, named after James G. Oldroyd, is the rate of change of some tensor property of a small parcel of fluid that is written in the coordinate system rotating and stretching with the fluid.

The operator is specified by the following formula:

where:

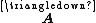• is the upper-convected time derivative of a tensor field
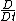• is the substantive derivative
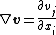• is the tensor of velocity derivatives for the fluid.

The formula can be rewritten as:

By definition the upper-convected time derivative of the Finger tensor is always zero.

It can be shown that the upper-convected time derivative of a spacelike vector field is just its Lie derivative by the velocity field of the continuum.^[1]

The upper-convected derivative is widely use in polymer rheology for the description of behavior of a viscoelastic fluid under large deformations.

Examples for the symmetric tensor A

Simple shear

For the case of simple shear:

Thus,

Uniaxial extension of incompressible fluid

In this case a material is stretched in the direction X and compresses in the directions Y and Z, so to keep volume constant.

The gradients of velocity are:

Thus,

See also

• Upper-convected Maxwell model

References

• {{cite book | author=Macosko, Christopher| title=Rheology. Principles, Measurements and Applications | publisher=VCH Publisher | year=1993 | isbn=978-1-56081-579-2}}

Notes

• Gowan, James
• Gowan, Lawrence
• GoWansbeck
• Go Wansbeck
• Gowan's Copper
• Gowan's copper
• Gowans, William
• Gowanus Batcave
• Gowara
• Gowarikar
• Gowariker
• GoWarrior
• GoWarrior computing platform
• Gowa Sultanate
• Gowda
• Gowda (caste)
• Gowda (disambiguation)
• Gowda, James
• Gowda(surname)
• Gow, David
• Gowdeyana
• Gowdeyana punctifera
• Gowdy, Indiana
• Go (Weeds)
• Gowen City