“Van Wijngaarden transformation”的意思、由来-开放百科全书

词条

Van Wijngaarden transformation

释义

References
See also

In mathematics and numerical analysis, in order to accelerate convergence of an alternating series, Euler's transform can be computed as follows.

Compute a row of partial sums :

and form rows of averages between neighbors,

The first column 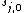then contains the partial sums of the Euler transform.

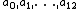Adriaan van Wijngaarden's contribution was to point out that it is better not to carry this procedure through to the very end, but to stop two-thirds of the way.^[1] If

are available, then

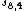is almost always a better approximation to the sum than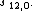

Leibniz formula for pi, 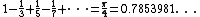, gives the partial sum , the Euler transform partial sum 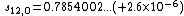and the van Wijngaarden result 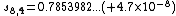(relative errors are in round brackets).

 1.00000000 0.66666667 0.86666667 0.72380952 0.83492063 0.74401154 0.82093462 0.75426795 0.81309148 0.76045990 0.80807895 0.76460069 '''0.80460069''' 0.83333333 0.76666667 0.79523810 0.77936508 0.78946609 0.78247308 0.78760129 0.78367972 0.78677569 0.78426943 0.78633982 0.78460069  0.80000000 0.78095238 0.78730159 0.78441558 0.78596959 0.78503719 0.78564050 0.78522771 0.78552256 0.78530463 0.78547026  0.79047619 0.78412698 0.78585859 0.78519259 0.78550339 0.78533884 0.78543410 0.78537513 0.78541359 0.78538744  0.78730159 0.78499278 0.78552559 0.78534799 0.78542111 0.78538647 0.78540462 0.78539436 0.78540052  0.78614719 0.78525919 0.78543679 0.78538455 0.78540379 0.78539555 0.78539949 0.78539744  0.78570319 0.78534799 0.78541067 0.78539417 0.78539967 0.78539752 0.78539847  0.78552559 0.78537933 0.78540242 0.78539692 0.78539860 0.78539799  0.78545246 0.78539087 0.78539967 0.78539776 '''0.78539829'''  0.78542166 0.78539527 0.78539871 0.78539803  0.78540847 0.78539699 0.78539837  0.78540273 0.78539768      '''0.78540021'''

This table results from the J formula 'b11.8'8!:2-:&(}:+}.)^:n+/\\(_1^n)*%1+2*n=.i.13 In many cases the diagonal terms do not converge in one cycle so process of averaging is to be repeated with diagonal terms by bringing them in a row. This will be needed in a geometric series with ratio -4. This process of successive averaging of the average of partial sum can be replaced by using formula to calculate the diagonal term.

References

1. ^A. van Wijngaarden, in: Cursus: Wetenschappelijk Rekenen B, Proces Analyse, Stichting Mathematisch Centrum, (Amsterdam, 1965) pp. 51-60

References

See also