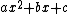“Vertex (curve)”的意思、由来-开放百科全书

词条

Vertex (curve)

释义

Examples
Cusps and osculation
Other properties
Notes
References

In the geometry of planar curves, a vertex is a point of where the first derivative of curvature is zero.^[1] This is typically a local maximum or minimum of curvature,^[2] and some authors define a vertex to be more specifically a local extreme point of curvature.^[2] However, other special cases may occur, for instance when the second derivative is also zero, or when the curvature is constant. For space curves, on the other hand, a vertex is a point where the torsion vanishes.

Examples

A hyperbola has two vertices, one on each branch; they are the closest of any two points lying on opposite branches of the hyperbola, and they lie on the principal axis. On a parabola, the sole vertex lies on the axis of symmetry and in a quadratic of the form:

it can be found by completing the square or by differentiation.^[3] On an ellipse, two of the four vertices lie on the major axis and two lie on the minor axis.^[4]

For a circle, which has constant curvature, every point is a vertex.

Cusps and osculation

Vertices are points where the curve has 4-point contact with the osculating circle at that point.^[5]^[6] In contrast, generic points on a curve typically only have 3-point contact with their osculating circle. The evolute of a curve will generically have a cusp when the curve has a vertex;^[6] other, more degenerate and non-stable singularities may occur at higher-order vertices, at which the osculating circle has contact of higher order than four.^[5] Although a single generic curve will not have any higher-order vertices, they will generically occur within a one-parameter family of curves, at the curve in the family for which two ordinary vertices coalesce to form a higher vertex and then annihilate.

The symmetry set of a curve has endpoints at the cusps corresponding to the vertices, and the medial axis, a subset of the symmetry set, also has its endpoints in the cusps.

Other properties

According to the classical four-vertex theorem, every simple closed planar smooth curve must have at least four vertices.^[7] A more general fact is that every simple closed space curve which lies on the boundary of a convex body, or even bounds a locally convex disk, must have four vertices.^[8]

If a planar curve is bilaterally symmetric, it will have a vertex at the point or points where the axis of symmetry crosses the curve. Thus, the notion of a vertex for a curve is closely related to that of an optical vertex, the point where an optical axis crosses a lens surface.

Notes

1. ^{{harvtxt|Agoston|2005}}, p. 570; {{harvtxt|Gibson|2001}}, p. 126.
2. ^{{harvtxt|Fuchs|Tabachnikov|2007}}, p. 141.
3. ^¹{{harvtxt|Gibson|2001}}, p. 127.
4. ^{{harvtxt|Agoston|2005}}, p. 570; {{harvtxt|Gibson|2001}}, p. 127.
5. ^¹{{harvtxt|Gibson|2001}}, p. 126.
6. ^¹{{harvtxt|Fuchs|Tabachnikov|2007}}, p. 142.
7. ^{{harvtxt|Agoston|2005}}, Theorem 9.3.9, p. 570; {{harvtxt|Gibson|2001}}, Section 9.3, "The Four Vertex Theorem", pp. 133–136; {{harvtxt|Fuchs|Tabachnikov|2007}}, Theorem 10.3, p. 149.
8. ^{{harvtxt|Sedykh|1994}}; {{harvtxt|Ghomi|2015}}

References

{{citation|title=Computer Graphics and Geometric Modelling: Mathematics|first=Max K.|last=Agoston|publisher=Springer|year=2005|isbn=9781852338176}}.
{{citation|title=Mathematical Omnibus: Thirty Lectures on Classic Mathematics|first1=D. B.|last1=Fuchs|authorlink1=Dmitry Fuchs|first2=Serge|last2=Tabachnikov|authorlink2=Sergei Tabachnikov|publisher=American Mathematical Society|year=2007|isbn=9780821843161}}
{{citation |last1=Ghomi|first1=Mohammad|title=Boundary torsion and convex caps of locally convex surfaces|arxiv= 1501.07626|date=2015|bibcode=2015arXiv150107626G}}
{{citation|title=Elementary Geometry of Differentiable Curves: An Undergraduate Introduction|first=C. G.|last=Gibson|publisher=Cambridge University Press|year=2001|isbn=9780521011075}}.
{{citation|last1=Sedykh|first1=V.D.|title=Four vertices of a convex space curve|journal=Bull. London Math. Soc.|date=1994|volume=26|issue=2|page=177–180}}

1 : Curves

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。