“Von Mises–Fisher distribution”的意思、由来-开放百科全书

词条

Von Mises–Fisher distribution

释义

Estimation of parameters
Generalizations
See also
References

In directional statistics, the von Mises–Fisher distribution (named after Ronald Fisher and Richard von Mises), is a

probability distribution on the

-dimensional sphere in

. If

the distribution reduces to the von Mises distribution on the circle.

The probability density function of the von Mises–Fisher distribution for the random p-dimensional unit vector is given by:

where and

the normalization constant is equal to

where denotes the modified Bessel function of the first kind at order . If , the normalization constant reduces to

The parameters and are called the mean direction and concentration parameter, respectively. The greater the value of , the higher the concentration of the distribution around the mean direction . The distribution is unimodal for 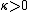, and is uniform on the sphere for .

The von Mises–Fisher distribution for , also called the Fisher distribution, was first used to model the interaction of electric dipoles in an electric field (Mardia, 2000). Other applications are found in geology, bioinformatics, and text mining.

Estimation of parameters

A series of N independent measurements are drawn from a von Mises–Fisher distribution. Define

Then (Sra, 2011) the maximum likelihood estimates of and are given by

Thus is the solution to

A simple approximation to is

but a more accurate measure can be obtained by iterating the Newton method a few times

For N ≥ 25, the estimated spherical standard error of the sample mean direction can be computed as^[1]

where

It's then possible to approximate a confidence cone about with semi-vertical angle

where

For example, for a 95% confidence cone, and thus

Generalizations

The matrix von Mises-Fisher distribution has the density

supported on the Stiefel manifold of orthonormal p-frames , where is an arbitrary real matrix.^[2]^[3]

References

1. ^{{cite book|last=Embleton|first=N. I. Fisher, T. Lewis, B. J. J.|title=Statistical analysis of spherical data|year=1993|publisher=Cambridge University Press|location=Cambridge|isbn=0-521-45699-1|pages=115–116|edition=1st pbk.}}
2. ^{{cite journal | last1 = Jupp | first1 = | year = 1979 | title = Maximum likelihood estimators for the matrix von Mises-Fisher and Bingham distributions | url = https://projecteuclid.org/euclid.aos/1176344681 | journal = The Annals of Statistics | volume = 7 | issue = 3 | pages = 599–606 | doi = 10.1214/aos/1176344681 }}
3. ^{{cite journal | last1 = Downs | first1 = | year = 1972 | title = Orientational statistics | url = | journal = Biometrika | volume = 59 | issue = | pages = 665–676 | doi=10.1093/biomet/59.3.665}}

Dhillon, I., Sra, S. (2003) "Modeling Data using Directional Distributions". Tech. rep., University of Texas, Austin.
Banerjee, A., Dhillon, I. S., Ghosh, J., & Sra, S. (2005). "Clustering on the unit hypersphere using von Mises-Fisher distributions". Journal of Machine Learning Research, 6(Sep), 1345-1382.
Fisher, RA, "Dispersion on a sphere'". (1953) Proc. Roy. Soc. London Ser. A., 217: 295–305
{{cite book |title=Directional Statistics |last=Mardia |first=Kanti |authorlink=Kantilal Mardia |last2 = Jupp | first2 = P. E.|year=1999 |publisher=Wiley |isbn=978-0-471-95333-3}}
{{Cite journal | last1 = Sra | first1 = S. | doi = 10.1007/s00180-011-0232-x | title = A short note on parameter approximation for von Mises-Fisher distributions: And a fast implementation of I s (x) | journal = Computational Statistics | volume = 27 | pages = 177–190 | year = 2011 | pmid = | pmc = | citeseerx = 10.1.1.186.1887}}

4 : Directional statistics|Multivariate continuous distributions|Exponential family distributions|Continuous distributions

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。

Estimation of parameters

Generalizations

See also

References