贝努利公式beinuli songshi

在贝努利概型中，在每次试验时，事件A发生的概率为p，不发生的概率为g=1-p，则在n次试验中事件A恰好发生k (0≤k≤n) 次的概率为：

此式称为贝努利公式。因为C_n^kp^kq^n-k恰好是二项式(p+g)ⁿ的展开式中的第k+1项，所以上式又称二项概率公式。
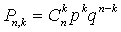
当n与k很大时，有近似公式

式中
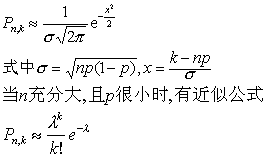
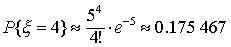
当n充分大，且p很小时，有近似公式

式中λ=np，把这个公式称为泊松公式。
例如，对同一目标进行独立射击4次，每次射中目标的概率为p，而射不中目标的概率为g=1-p。求在4次射击中，射中目标2次的概率。这个问题是属于四重贝努利试验。设A表示 “4次射击中，射中目标2次” A_i表示 “第i次射击，击中目标”。于是

则P (A) =C₄²p²q^4-2。
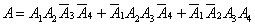
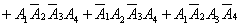
又如，在生产某产品过程中出现次品的概率是0. 005。今任意抽取1000件，求其中恰好有4件次品的概率。
设ξ表示为1000件产品中所含次品的件数，则P {ξ=4} =C⁴₁₀₀₀₄ (0.005)4 (0.995)996。直接计算这个结果十分麻烦.此时，n较大。p值很小，故可用泊松公式，计算得到近似值

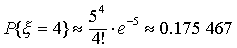
其中λ=np=1 000×0. 005=5,k=4。