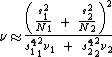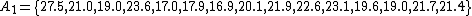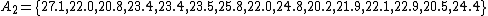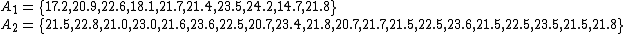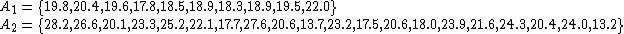- Assumptions
- Calculations
- Statistical test
- Advantages and limitations
- Examples
- Software implementations
- See also
- References
In statistics, Welch's t-test, or unequal variances t-test, is a two-sample location test which is used to test the hypothesis that two populations have equal means. It is named for its creator, Bernard Lewis Welch, and is an adaptation of Student's t-test,[1] and is more reliable when the two samples have unequal variances and/or unequal sample sizes.[2][3] These tests are often referred to as "unpaired" or "independent samples" t-tests, as they are typically applied when the statistical units underlying the two samples being compared are non-overlapping. Given that Welch's t-test has been less popular than Student's t-test[2] and may be less familiar to readers, a more informative name is "Welch's unequal variances t-test" or "unequal variances t-test" for brevity.[3]
Assumptions
Student's t-test assumes that the two populations have normal distributions with equal variances. Welch's t-test is designed for unequal variances, but the assumption of normality is maintained.[1] Welch's t-test is an approximate solution to the Behrens–Fisher problem.
Calculations
Welch's t-test defines the statistic t by the following formula:
where 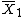 ,
,  and
and  are the 1st sample mean, sample variance and sample size, respectively. Unlike in Student's t-test, the denominator is not based on a pooled variance estimate.
are the 1st sample mean, sample variance and sample size, respectively. Unlike in Student's t-test, the denominator is not based on a pooled variance estimate.
The degrees of freedom  associated with this variance estimate is approximated using the Welch–Satterthwaite equation:
associated with this variance estimate is approximated using the Welch–Satterthwaite equation:
Here  , the degrees of freedom associated with the first variance estimate.
, the degrees of freedom associated with the first variance estimate.  , the degrees of freedom associated with the 2nd variance estimate.
, the degrees of freedom associated with the 2nd variance estimate.
Statistical test
Once t and  have been computed, these statistics can be used with the t-distribution to test one of two possible null hypotheses:
have been computed, these statistics can be used with the t-distribution to test one of two possible null hypotheses:
- that the two population means are equal, in which a two-tailed test is applied; or
- that one of the population means is greater than or equal to the other, in which a one-tailed test is applied.
Advantages and limitations
Welch's t-test is more robust than Student's t-test and maintains type I error rates close to nominal for unequal variances and for unequal sample sizes under normality. Furthermore, the power of Welch's t-test comes close to that of Student's t-test, even when the population variances are equal and sample sizes are balanced.[2] Welch's t-test can be generalized to more than 2-samples,[4] which is more robust than one-way analysis of variance (ANOVA).
It is not recommended to pre-test for equal variances and then choose between Student's t-test or Welch's t-test.[5] Rather, Welch's t-test can be applied directly and without any substantial disadvantages to Student's t-test as noted above. Welch's t-test remains robust for skewed distributions and large sample sizes.[6] Reliability decreases for skewed distributions and smaller samples, where one could possibly perform Welch's t-test on ranked data.[7]
Examples
The following three examples compare Welch's t-test and Student's t-test. Samples are from random normal distributions using the R programming language.
For all three examples, the population means were  and
and  .
.
The first example is for equal variances ( ) and equal sample sizes (
) and equal sample sizes (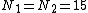 ). Let A1 and A2 denote two random samples:
). Let A1 and A2 denote two random samples:
The second example is for unequal variances ( ,
,  ) and unequal sample sizes (
) and unequal sample sizes ( ,
, 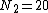 ). The smaller sample has the larger variance:
). The smaller sample has the larger variance:
The third example is for unequal variances ( ,
,  ) and unequal sample sizes (
) and unequal sample sizes ( ,
, 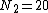 ). The larger sample has the larger variance:
). The larger sample has the larger variance:
Reference p-values were obtained by simulating the distributions of the t statistics for the null hypothesis of equal population means ( ). Results are summarised in the table below, with two-tailed p-values:
). Results are summarised in the table below, with two-tailed p-values:
| Sample A1 | Sample A2 | Student's t-test | Welch's t-test | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Example |  | 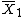 |  |  |  |  | {{tmath|t | {{tmath|\u | {{tmath|P |  | {{tmath|t | {{tmath|\u | {{tmath|P |  |
| 1 | 15 | 20.8 | 7.9 | 15 | 23.0 | 3.8 | −2.46 | 28 | 0.021 | 0.021 | −2.46 | 25.0 | 0.021 | 0.017 |
| 2 | 10 | 20.6 | 9.0 | 20 | 22.1 | 0.9 | −2.10 | 28 | 0.045 | 0.150 | −1.57 | 9.9 | 0.149 | 0.144 |
| 3 | 10 | 19.4 | 1.4 | 20 | 21.6 | 17.1 | −1.64 | 28 | 0.110 | 0.036 | −2.22 | 24.5 | 0.036 | 0.042 |
Welch's t-test and Student's t-test gave identical results when the two samples have identical variances and sample sizes (Example 1). But note that if you sample data from populations with identical variances, the sample variances will differ, as will the results of the two t-tests. So with actual data, the two tests will almost always give somewhat different results.
For unequal variances, Student's t-test gave a low p-value when the smaller sample had a larger variance (Example 2) and a high p-value when the larger sample had a larger variance (Example 3). For unequal variances, Welch's t-test gave p-values close to simulated p-values.
Software implementations
| Language/Program | Function | Notes |
|---|---|---|
| LibreOffice | TTEST(Data1; Data2; Mode; Type) | See [https://help.libreoffice.org/Calc/Statistical_Functions_Part_Five#TTEST] |
| MATLAB | ttest2(data1, data2, 'Vartype', 'unequal') | See |
| Microsoft Excel pre 2010 | TTEST(array1, array2, tails, type) | See |
| Microsoft Excel 2010 and later | T.TEST(array1, array2, tails, type) | See |
| Minitab | Access commands through menu: see [8] | [9] |
| SAS (Software) | default output from proc ttest (labeled "Satterthwaite") | |
| Python | scipy.stats.ttest_ind(a, b, axis=0, equal_var=False) | See |
| R | t.test(data1, data2, alternative="two.sided", var.equal=FALSE) | See [https://stat.ethz.ch/R-manual/R-devel/library/stats/html/t.test.html] |
| Haskell | Statistics.Test.StudentT.welchTTest SamplesDiffer data1 data2 | See |
| JMP | Oneway( Y( YColumn), X( XColumn), Unequal Variances( 1 ) ); | See [https://www.jmp.com/support/help/] |
| Julia | UnequalVarianceTTest(data1, data2) | See |
| Stata | ttest varname1 == varname2, welch | See |
| Google Sheets | TTEST(range1, range2, tails, type) | See [https://support.google.com/docs/answer/6055837?hl=en] |
| GraphPad Prism | It is a choice on the t test dialog. | |
| IBM SPSS Statistics | An option in the menu | [10]. Cf. [11] |
See also
{{Portal|Statistics}}- Student's t-test
- Z-test
- Factorial experiment
- One-way analysis of variance
- Hotelling's two-sample T-squared statistic, a multivariate extension of Welch's t-test
References
2. ^1 2 {{Cite journal | last = Ruxton | first = G. D. | title = The unequal variance t-test is an underused alternative to Student's t-test and the Mann–Whitney U test |journal = Behavioral Ecology | volume = 17 | pages = 688–690 | year = 2006 | doi = 10.1093/beheco/ark016}}
3. ^1 {{cite journal|last1=Derrick|first1=B|last2=Toher|first2=D|last3=White|first3=P|title=Why Welchs test is Type I error robust|journal=The Quantitative Methods for Psychology|date=2016|volume=12|issue=1|pages=30-38|doi=10.20982/tqmp.12.1.p030|url=http://eprints.uwe.ac.uk/27232/27/p030.pdf}}
4. ^{{cite journal|last1=Welch|first1=B. L.|title=On the Comparison of Several Mean Values: An Alternative Approach|journal=Biometrika|date=1951|volume=38|pages=330–336|doi=10.2307/2332579|jstor=2332579}}
5. ^{{Cite journal | last = Zimmerman | first = D. W. | title = A note on preliminary tests of equality of variances | journal = British Journal of Mathematical and Statistical Psychology | volume = 57 | pages = 173–181 | year = 2004 | doi = 10.1348/000711004849222}}
6. ^{{Cite journal | last = Fagerland | first = M. W. | title = t-tests, non-parametric tests, and large studies—a paradox of statistical practice? | journal = BioMed Central Medical Research Methodology | volume = 12 | pages = 78 | year = 2012 | doi = 10.1186/1471-2288-12-78}}
7. ^{{Cite journal | last1 = Fagerland | first1 = M. W. | last2 = Sandvik | first2 = L. | title = Performance of five two-sample location tests for skewed distributions with unequal variances | journal = Contemporary Clinical Trials | volume = 30 | pages = 490–496 | year = 2009 | doi=10.1016/j.cct.2009.06.007}}
8. ^Example of 2-Sample t - Minitab: — official documentation for Minitab version 18. Accessed 2019-01-22.
9. ^Select the analysis options for 2-Sample t - Minitab: — official documentation for Minitab version 18. Accessed 2019-01-22.
10. ^Jeremy Miles (https://stats.stackexchange.com/users/17072/jeremy-miles), Unequal variances t-test or U Mann-Whitney test?, URL (version: 2014-04-11): https://stats.stackexchange.com/q/93475
11. ^[https://www.ibm.com/support/knowledgecenter/SSLVMB_24.0.0/spss/base/syn_t-test_examples.html#syn_t-test_examples ] — Official documentation for SPSS Statistics version 24. Accessed 2019-01-22.
- Estrin (compound)
- Estrin, James
- Estrins
- Estriol 16-glucuronide 3-sulfate
- Estriol 16α-glucuronide
- Estriol 16α-glucuronide 3-sulfate
- Estriol 17-phosphate
- Estriol 17β-phosphate
- Estriol 3,17β-dihexanoate
- Estriol 3,17β-dipropionate
- Estriol 3-cyclopentyl ether
- Estriol 3-glucuronide
- Estriol-3-O-sulfamate
- Estriol 3-O-sulfamate
- Estriol 3-sulfamate
- Estriol-3-sulfamate
- Estriol 3-sulfate
- Estriol 3-sulfate 16-glucuronide
- Estriol 3-sulfate 16α-glucuronide
- Estriol 3-β-D-glucosiduronic acid
- Estriol acetate benzoate
- Estriol conjugate
- Estriol conjugates
- Estriol cyclopentyl ether
- Estriol derivative