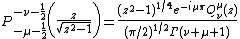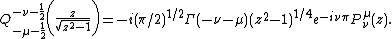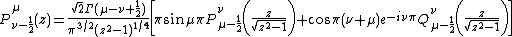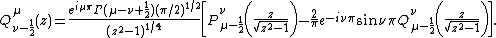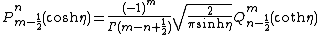“Whipple formulae”的意思、由来-开放百科全书

词条

Whipple formulae

释义

External links
References

In the theory of special functions, Whipple's transformation for Legendre functions, named after Francis John Welsh Whipple, arise from a general expression, concerning associated Legendre functions. These formulae have been presented previously in terms of a viewpoint aimed at spherical harmonics, now that we view the equations in terms of toroidal coordinates, whole new symmetries of Legendre functions arise.

For associated Legendre functions of the first and second kind,

and

These expressions are valid for all parameters 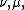and . By shifting the complex degree and order in an appropriate fashion, we obtain Whipple formulae for general complex index interchange of general associated Legendre functions of the first and second kind. These are given by

and

Note that these formulae are well-behaved for all values of the degree and order, except for those with integer values. However, if we examine these formulae for toroidal harmonics, i.e. where the degree is half-integer, the order is integer, and the argument is positive and greater than unity one obtains

and

.

These are the Whipple formulae for toroidal harmonics. They show an important property of toroidal harmonics under index (the integers associated with the order and the degree) interchange.

External links

References

{{cite journal | last=Cohl | first=Howard S. |author2=J.E. Tohline |author3=A.R.P. Rau |author4=H.M. Srivastava | title=Developments in determining the gravitational potential using toroidal functions | year=2000 | journal=Astronomische Nachrichten | volume=321 | issue=5/6 | pages=363–372 | doi=10.1002/1521-3994(200012)321:5/6<363::AID-ASNA363>3.0.CO;2-X|bibcode = 2000AN....321..363C }}

1 : Special functions

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。