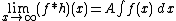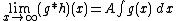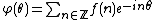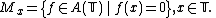“Wiener's tauberian theorem”的意思、由来-开放百科全书

词条

Wiener's tauberian theorem

释义

The condition in {{math|L₁}}
Tauberian reformulation Discrete version
The condition in {{math|L₂}}
Notes
References
External links

In mathematical analysis, Wiener's tauberian theorem is any of several related results proved by Norbert Wiener in 1932.^[1] They provide a necessary and sufficient condition under which any function in {{math|L₁}} or {{math|L₂}} can be approximated by linear combinations of translations of a given function.^[2]

Informally, if the Fourier transform of a function {{math|f}} vanishes on a certain set {{math|Z}}, the Fourier transform of any linear combination of translations of {{math|f}} also vanishes on {{math|Z}}. Therefore, the linear combinations of translations of {{math|f}} can not approximate a function whose Fourier transform does not vanish on {{math|Z}}.

Wiener's theorems make this precise, stating that linear combinations of translations of {{math|f}} are dense if and only if the zero set of the Fourier transform of {{math|f}} is empty (in the case of {{math|L₁}}) or of Lebesgue measure zero (in the case of {{math|L₂}}).

Gelfand reformulated Wiener's theorem in terms of commutative C*-algebras, when it states that the spectrum of the L¹ group ring L¹(R) of the group R of real numbers is the dual group of R. A similar result is true when R is replaced by any locally compact abelian group.

The condition in {{math|L₁}}

Let {{math|f ∈ L₁(R)}} be an integrable function. The span of translations {{math|f_a(x)}} = {{math|f(x + a)}} is dense in {{math|L₁(R)}} if and only if the Fourier transform of {{math|f}} has no real zeros.

Tauberian reformulation

The following statement is equivalent to the previous result,{{Citation needed|date=October 2018}} and explains why Wiener's result is a Tauberian theorem:

Suppose the Fourier transform of {{math|f ∈ L₁}} has no real zeros, and suppose the convolution {{math|f * h}} tends to zero at infinity for some {{math|h ∈ L_∞}}. Then the convolution {{math|g * h}} tends to zero at infinity for any {{math|g ∈ L₁}}.

More generally, if

for some {{math|f ∈ L₁}} the Fourier transform of which has no real zeros, then also

for any {{math|g ∈ L₁}}.

Discrete version

Wiener's theorem has a counterpart in {{math|l₁(Z)}}: the span of the translations of {{math|f ∈ l₁(Z)}} is dense if and only if the Fourier transform

has no real zeros. The following statements are equivalent version of this result:

Suppose the Fourier transform of {{math|f ∈ l₁(Z)}} has no real zeros, and for some bounded sequence {{math|h}} the convolution {{math|f h}} tends to zero at infinity. Then {{math|g h}} also tends to zero at infinity for any {{math|g ∈ l₁(Z)}}.
Let {{math|φ}} be a function on the unit circle with absolutely convergent Fourier series. Then {{math|1/φ}} has absolutely convergent Fourier series if and only if {{math|φ}} has no zeros.

{{harvs|txt|last=Gelfand|author-link=Israel Gelfand|year1=1941a|year2=1941b}} showed that this is equivalent to the following property of the Wiener algebra {{math|A(T)}}, which he proved using the theory of Banach algebras, thereby giving a new proof of Wiener's result:

The maximal ideals of {{math|A(T)}} are all of the form

The condition in {{math|L₂}}

Let {{math|f ∈ L₂(R)}} be a square-integrable function. The span of translations {{math|f_a(x)}} = {{math|f(x + a)}} is dense in {{math|L₂(R)}} if and only if the real zeros of the Fourier transform of {{math|f}} form a set of zero Lebesgue measure.

The parallel statement in {{math|l₂(Z)}} is as follows: the span of translations of a sequence {{math|f ∈ l₂(Z)}} is dense if and only if the zero set of the Fourier transform

has zero Lebesgue measure.

Notes

1. ^See {{harvtxt|Wiener|1932}}.
2. ^see {{harvtxt|Rudin|1991}}.

References

{{Citation | last1=Gelfand | first1=I. | author-link=Israel Gelfand|title=Normierte Ringe | year=1941a | journal=Rec. Math. (Mat. Sbornik) N.S.| volume=9 | issue = 51 | pages=3–24 | mr=0004726}}
{{Citation | last1=Gelfand | first1=I. | author-link=Israel Gelfand|title=Über absolut konvergente trigonometrische Reihen und Integrale | year=1941b | journal=Rec. Math. (Mat. Sbornik) N.S.| volume=9 | issue = 51 | pages=51–66 | mr=0004727}}
{{Citation | mr=1157815 | last=Rudin | first = W.| author-link=Walter Rudin|title=Functional analysis|series=International Series in Pure and Applied Mathematics|publisher=McGraw-Hill, Inc.|location=New York|year=1991|isbn=0-07-054236-8}}
{{Citation | last=Wiener|first=N.|author-link=Norbert Wiener|title=Tauberian Theorems|journal=Annals of Mathematics|volume=33|issue=1|year=1932|pages=1–100|jstor=1968102}}

External links

{{eom|id=W/w097950|title=Wiener Tauberian theorem|first=A.I.|last=Shtern}}

3 : Real analysis|Harmonic analysis|Tauberian theorems

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。

The condition in {{math|L1}}