轨迹交截法guiji jiaojiefa

用轨迹确定一个点的位置的方法.若解决一个作图题归结起来是要确定某一个点的位置，则可以暂时放弃这点所满足的条件之一，于是满足其余条件的点可形成一个轨迹；这时再改换放弃另一个条件，又得到一个轨迹，所求的点应在这两个轨迹上.因此，两个轨迹的交点就是所求的点.象这样利用轨迹的交点来解作图题的方法，叫做轨迹交截法或轨迹交点法（简称轨迹法）.
例如，已知三角形的一边，这边所对的角及这边上的高，求作三角形.
已知 线段a,h和∠a.

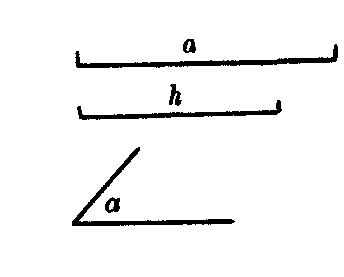
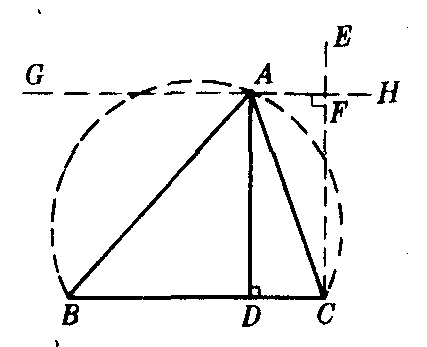
求作 △ABC，使BC=a,∠A=a,BC边上的高线等于h.
分析 如图，假定△ABC为所求的三角形.BC=a,∠A=a，高线AD=h.边BC可以先作出.也就是B,C两点的位置可以先确定.因为A点距离定直线BC为定长h.所以它的轨迹是距BC等于h的平行线GH（第一轨迹）.又因为∠A的大小一定，两边通过二定点B,C，所以它的轨迹是以BC为弦，含角a的弓形弧（第二轨迹）.这两个轨迹的交点就是A点的位置.于是△ABC可作.
作法 ❶作线段BC=a;
❷过C作CE⊥BC，在CE上取CF=h，过F作GH∥BC;
❸以BC为弦作弓形弧，使它所含的弓形角等于a.交GH于A;
❹连结AB,AC.则△ABC就是所求的三角形.
证明 略.
讨论 当GH和弓形弧相交时，本题有一解；当GH和弓形弧相切时，本题也有一解，此时所求的三角形为等腰三角形；当GH和弓形弧相离时，本题无解.