辗转相除法zhanzhuan xiangchu fa
我国古代数学家创造的一种算法.但在外文书籍中通常把它叫做欧几里得算法.辗转相除法的具体做法如下:设a,b是任意两个正整数,由带余数除法定理,我们可得下列等式:
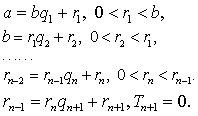
辗转相除法在求最大公因数,最小公倍数,解一次不定方程,解一次同余式以及求连分数展开式等都有重要应用.
辗转相除法Zhanzhuan xiangchufa
求两个数的最大公约数的一般方法。其步骤如下:设a和b是两个自然数,a>b, 先用b除a得商数q3和余数r1; 如果r1≠0,那么r11除b,得商数q2和余数r2;如果r2≠0,那么r2
a=bq1+r1,b=r1q2+r2,r1 = r2q3 +r3,
rk-2 =rk-1qk+rkrk-1 =rkqk+1,
那么,rk也就是最后一个除数,就是a和b的最大公约数, 即rk= (a, b)。例: 求 (143, 221)。221÷143=1 (余78), 即221=143·1+78; 143÷78=1(余65),即143=78·1+65;78÷65=1(余13),即78=65·1+13; 65÷13=5(余0),即65=13·5。那么, (143, 221) =13。
辗转相除法
一种带余除法。给定过程如下:整数a>0,b>0。可得到
a=bq1+r1,0
r1=r2q3+r3,0
… …
rn-2=rn-1qn+rn,0
rn-1=rnqn+1+rn+1,rn+1=0
即经过有限次除法,总可得到一个余数等于零。可用此法求最大公约数。对于给定的两个多项式f(x),g(x),也可类似地利用辗转相除法求最大公因式。