连分数lianfenshu
设{an)(n=0,1,2，…，m),{bn}(n=1,2，…，m)是由某域F中的元素所组成的有穷序列，则形如
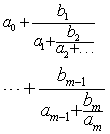
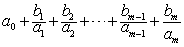
| 或者简记为 |
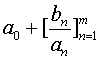
| 当{ax}、{bx}为无穷序列时，表达式 |
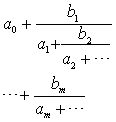
| 称为无限连分数，可以简记为 |
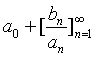
| 或者简记为 |
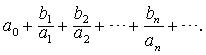
有尽连分数总可以从最下面一个分数开始逐步化简，最终总是域F中的一个元素.
无限连分数中，fn＝a0+[bk/ak]kn=1称为此连分数的第n个渐近分数，f0＝a0称为初项.若F是拓扑域(如R,C)且
fn存在，则称此无限连分数收敛，其极限值称为这个连分数的值.其第n个渐近分数之值称为这个连分数的n级(或n阶)近似值.连分数
是由两组数列a0,a1，…及b1,b2，…所组成的表达式简记为a0+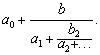
称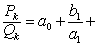
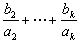为该连分数的第k个渐近分数。如果数列
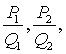…的极限存在，称此连分数收敛，极限称为连分数的值。任意实数都可以用一个连分数来表示。