连通liantong

无向图G中，若点u,v之间存在路，则称u,v是连通的.若无向图G的任意二点都是连通的，则G称为连通图.
若认为无向图G的任意点“自身是连通的，则无向图G中点的连通关系是点集的一个等价关系，即适合自反性、对称性、传递性的关系. 于是，G的点集V能划分成互不相交的子集V₁,V₂，…，V_k的并； V₁ ∪V₂ ∪…∪V_k＝V,i≠j,V_i∩V_j＝φ.不同的V_i,V_j，中的点互不连通，而同一V_i中的点彼此连通.每个V _i的点及它们关联的边构成G的子图G_i，称为G的一个连通分支； W (G) =k称为G的连通分支数，当W (G)=1时，称G是连通图.
无向连通图的这两个定义是等价的.
对于有向图G来说，若存在u到v的有向路，则说u可达v. 当然，u可达v时，未必u可达v.有向图G的任意二点都相互可达时，G称为强连通的；若G的任意二点，至少有一点可达另一点，则G称为单侧连通的；若G略去边的方向时是连通图； 则弥G是弱连通的. 强连通图必是单侧连通图； 单侧连通图必是弱连通图. 其逆均不真.
例如图

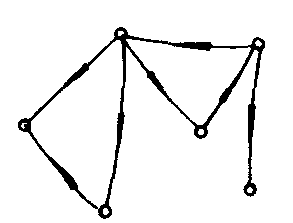
G₁

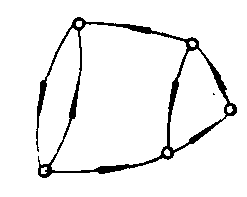
G₂

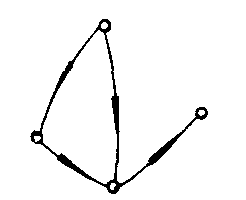
G₃