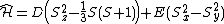- Quantum mechanical description Algebraic derivation
- References
- Further reading
- External links
The classic case for ZFS is the spin triplet, i.e., the S=1 spin system. In the presence of a magnetic field, the levels with different values of magnetic spin quantum number (MS=0,±1) are separated and the Zeeman splitting dictates their separation. In the absence of magnetic field, the 3 levels of the triplet are isoenergetic to the first order. However, when the effects of inter-electron repulsions are considered, the energy of the three sublevels of the triplet can be seen to have separated. This effect is thus an example of ZFS. The degree of separation depends on the symmetry of the system.
Quantum mechanical description
The corresponding Hamiltonian can be written as:
Where S is the total spin quantum number, and 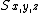 are the spin matrices.
are the spin matrices.
The value of the ZFS parameter are usually defined via D and E parameters. D describes the axial component of the magnetic dipole–dipole interaction, and E the transversal component. Values of D have been obtained for a wide number of organic biradicals by EPR measurements. This value may be measured by other magnetometry techniques such as SQUID; however, EPR measurements provide more accurate data in most cases. This value can also be obtained with other techniques such as optically detected magnetic resonance (ODMR; a double resonance technique which combines EPR with measurements such as fluorescence, phosphorescence and absorption), with sensitivity down to a single molecule or defect in solids like diamond (e.g. N-V center) or silicon carbide.
Algebraic derivation
The start is the corresponding Hamiltonian 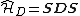 .
.  describes the dipolar spin-spin interaction between two unpaired spins (
describes the dipolar spin-spin interaction between two unpaired spins ( and
and  ). Where
). Where  is the total spin
is the total spin 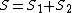 , and
, and  being a symmetric and traceless (which it is when
being a symmetric and traceless (which it is when  arises from dipole-dipole interaction) matrix, which means it is diagonalizable.
arises from dipole-dipole interaction) matrix, which means it is diagonalizable.
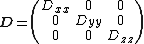 |{{EquationRef|1}}}}
|{{EquationRef|1}}}}with  being traceless (
being traceless (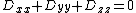 ). For simplicity
). For simplicity 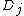 is defined as
is defined as 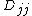 . The Hamiltonian becomes:
. The Hamiltonian becomes:
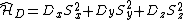 |{{EquationRef|2}}}}
|{{EquationRef|2}}}}The key is to express 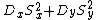 as its mean value and a deviation
as its mean value and a deviation 
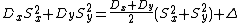 |{{EquationRef|3}}}}
|{{EquationRef|3}}}}To find the value for the deviation  which is then by rearranging equation ({{EquationNote|3}}):
which is then by rearranging equation ({{EquationNote|3}}):
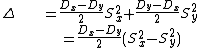 |{{EquationRef|4}}}}
|{{EquationRef|4}}}}By inserting ({{EquationNote|4}}) and ({{EquationNote|3}}) into ({{EquationNote|2}}) the result reads as:
{{NumBlk|:|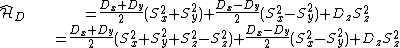 |{{EquationRef|5}}}}
|{{EquationRef|5}}}}Note, that in the second line in ({{EquationNote|5}})
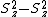 was added. By doing so
was added. By doing so  can be further used.
can be further used.
By using the fact, that  is traceless (
is traceless (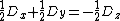 ) equation ({{EquationNote|5}}) simplifies to:
) equation ({{EquationNote|5}}) simplifies to:
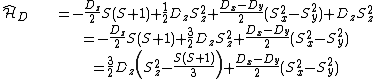 |{{EquationRef|6}}}}
|{{EquationRef|6}}}}By defining D and E parameters equation ({{EquationNote|6}}) becomes to:
{{NumBlk|:|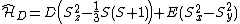 |{{EquationRef|7}}}}
|{{EquationRef|7}}}}with 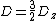 and
and 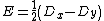 (measurable) zero field splitting values.
(measurable) zero field splitting values.
References
Further reading
- Principles of electron spin resonance: By N M Atherton. pp 585. Ellis Horwood PTR Prentice Hall. 1993 {{ISBN|0-137-21762-5}}
- {{cite journal |last=Christle |first=David J. |last2=et |first2=al |date=2015 |title=Isolated electron spins in silicon carbide with millisecond coherence times |url=http://www.nature.com/nmat/journal/v14/n2/full/nmat4144.html |journal=Nature Materials |volume=14 |issue=6 |pages=160–163 |doi=10.1038/nmat4144 |access-date=June 27, 2014 |pmid=25437259|arxiv=1406.7325 |bibcode=2015NatMa..14..160C }}
- {{cite journal |last=Widmann |first=Matthias |last2=et |first2=al |date=2015 |title=Coherent control of single spins in silicon carbide at room temperature |url=http://www.nature.com/nmat/journal/v14/n2/abs/nmat4145.html |journal=Nature Materials |volume=14 |issue=6 |pages=164–168 |doi=10.1038/nmat4145 |access-date=June 29, 2014 |pmid=25437256|arxiv=1407.0180 |bibcode=2015NatMa..14..164W }}
External links
- [https://web.archive.org/web/20110608062413/http://www.ncsu.edu/chemistry/das/zero-field_splitting.pdf Description of the origins of Zero Field Splitting]
- Konrad, Count Palatine of the Rhine
- Konrad der Rote
- Konrad der Rothe
- Konrad (disambiguation)
- Konrad Dobler
- Konrad, Duke of Meiningen
- Konrad Eberhard
- Konrad Elser
- Konrad Ernst Eduard Henlein
- Konrad Fehr
- Konrad Friedrich Hurlebusch
- Konrad Geßner
- Konrad Granstroem
- Konrad Granstrom
- Konrad Gröber
- Konrad H. Christ
- Konrad Hermann Josef Adenauer
- Konrad Heubeck
- Konrad Hirsch
- Konrad Huber
- Konrad Hupfer
- Konradia
- Konrad I, Bishop of Konstanz
- Konrad I, Count of Wuerttemberg
- Konrad I, Count of Wurttemberg