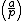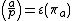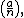“Zolotarev's lemma”的意思、由来-开放百科全书

词条

Zolotarev's lemma

释义

Proof
Another proof
Jacobi symbol
History
References
External links

In number theory, Zolotarev's lemma states that the Legendre symbol

for an integer a modulo an odd prime number p, where p does not divide a, can be computed as the sign of a permutation:

where ε denotes the signature of a permutation and π_a is the permutation of the nonzero residue classes mod p induced by multiplication by a.

For example, take a = 2 and p = 7. The nonzero squares mod 7 are 1, 2, and 4, so (2|7) = 1 and (6|7) = −1. Multiplication by 2 on the nonzero numbers mod 7 has the cycle decomposition (1,2,4)(3,6,5), so the sign of this permutation is 1, which is (2|7). Multiplication by 6 on the nonzero numbers mod 7 has cycle decomposition (1,6)(2,5)(3,4), whose sign is −1, which is (6|7).

Proof

In general, for any finite group G of order n, it is straightforward to determine the signature of the permutation π_g made by left-multiplication by the element g of G. The permutation π_g will be even, unless there are an odd number of orbits of even size. Assuming n even, therefore, the condition for π_g to be an odd permutation, when g has order k, is that n/k should be odd, or that the subgroup <g> generated by g should have odd index.

We will apply this to the group of nonzero numbers mod p, which is a cyclic group of order p − 1. The jth power of a primitive root modulo p will by index calculus have index the greatest common divisor

i = (j, p − 1).

The condition for a nonzero number mod p to be a quadratic non-residue is to be an odd power of a primitive root.

The lemma therefore comes down to saying that i is odd when j is odd, which is true a fortiori, and j is odd when i is odd, which is true because p − 1 is even (p is odd).

Another proof

Zolotarev's lemma can be deduced easily from Gauss's lemma and vice versa. The example

,

i.e. the Legendre symbol (a/p) with a = 3 and p = 11, will illustrate how the proof goes. Start with the set {1, 2, . . . , p − 1} arranged as a matrix of two rows such that the sum of the two elements in any column is zero mod p, say:

1	2	3	4	5
10	9	8	7	6

Apply the permutation :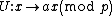

3	6	9	1	4
8	5	2	10	7

The columns still have the property that the sum of two elements in one column is zero mod p. Now apply a permutation V which swaps any pairs in which the upper member was originally a lower member:

3	5	2	1	4
8	6	9	10	7

Finally, apply a permutation W which gets back the original matrix:

1	2	3	4	5
10	9	8	7	6

We have W⁻¹ = VU. Zolotarev's lemma says (a/p) = 1 if and only if the permutation U is even. Gauss's lemma says (a/p) = 1 iff V is even. But W is even, so the two lemmas are equivalent for the given (but arbitrary) a and p.

Jacobi symbol

This interpretation of the Legendre symbol as the sign of a permutation can be extended to the Jacobi symbol

where a and n are relatively prime odd integers with n > 0: a is invertible mod n, so multiplication by a on Z/nZ is a permutation and a generalization of Zolotarev's lemma is that the Jacobi symbol above is the sign of this permutation.

For example, multiplication by 2 on Z/21Z has cycle decomposition (0)(1,2,4,8,16,11)(3,6,12)(5,10,20,19,17,13)(7,14)(9,18,15), so the sign of this permutation is (1)(−1)(1)(−1)(−1)(1) = −1 and the Jacobi symbol (2|21) is −1. (Note that multiplication by 2 on the units mod 21 is a product of two 6-cycles, so its sign is 1. Thus it's important to use all integers mod n and not just the units mod n to define the right permutation.)

When n = p is an odd prime and a is not divisible by p, multiplication by a fixes 0 mod p, so the sign of multiplication by a on all numbers mod p and on the units mod p have the same sign. But for composite n that is not the case, as we see in the example above.

History

This lemma was introduced by Yegor Ivanovich Zolotarev in an 1872 proof of quadratic reciprocity.

References

{{cite journal |author=Zolotareff G. |title=Nouvelle démonstration de la loi de réciprocité de Legendre |journal=Nouvelles Annales de Mathématiques|series= 2e série |volume=11 |year=1872 |pages=354–362 |url=http://archive.numdam.org/ARCHIVE/NAM/NAM_1872_2_11_/NAM_1872_2_11__354_0/NAM_1872_2_11__354_0.pdf}}

External links

[https://planetmath.org/zolotarevslemma PlanetMath article] on Zolotarev's lemma; includes his proof of quadratic reciprocity

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。