“41 equal temperament”的意思、由来-开放百科全书

词条

41 equal temperament

释义

History and use
Interval size
Tempering
References

In music, 41 equal temperament, abbreviated 41-TET, 41-EDO, or 41-ET, is the tempered scale derived by dividing the octave into 41 equally sized steps (equal frequency ratios). {{audio|41-tet scale on C.mid|Play}} Each step represents a frequency ratio of 2^1/41, or 29.27 cents ({{Audio|1 step in 41-et on C.mid|Play}}), an interval close in size to the septimal comma. 41-ET can be seen as a tuning of the schismatic,^[1] magic and miracle^[2] temperaments. It is the second smallest equal temperament, after 29-ET, whose perfect fifth is closer to just intonation than that of 12-ET. In other words, is a better approximation to the ratio 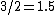than either or .

History and use

Although 41-ET has not seen as wide use as other temperaments such as 19-ET or 31-ET {{Citation needed|date=April 2008}}, pianist and engineer Paul von Janko built a piano using this tuning, which is on display at the Gemeentemuseum in The Hague.^[3] 41-ET can also be seen as an octave-based approximation of the Bohlen–Pierce scale.

41-ET is also a subset of 205-ET, for which the keyboard layout of the

Tonal Plexus is designed.

Interval size

Here are the sizes of some common intervals (shaded rows mark relatively poor matches):

interval name	size (steps)	size (cents)	midi	just ratio	just (cents)	midi	error
octave	41	1200		2:1	1200		0
harmonic seventh	33	965.85	{{Audio\|33 steps in 41-et on C.mid\|Play}}	7:4	968.83	{{Audio\|Harmonic seventh on C.mid\|Play}}	−2.97
perfect fifth	24	702.44	{{Audio\|24 steps in 41-et on C.mid\|Play}}	3:2	701.96	{{Audio\|Just perfect fifth on C.mid\|Play}}	+0.48
septimal tritone	20	585.37	{{Audio\|20 steps in 41-et on C.mid\|Play}}	7:5	582.51	{{Audio\|Lesser septimal tritone on C.mid\|Play}}	+2.85
11:8 wide fourth	19	556.10	{{Audio\|19 steps in 41-et on C.mid\|Play}}	11:8	551.32	{{Audio\|Eleventh harmonic on C.mid\|Play}}	+4.78
15:11 wide fourth	18	526.83	{{Audio\|18 steps in 41-et on C.mid\|Play}}	15:11	536.95	{{Audio\|Undecimal augmented fourth on C.mid\|Play}}	−10.12
27:20 wide fourth	18	526.83	{{Audio\|18 steps in 41-et on C.mid\|Play}}	27:20	519.55	{{audio\|Wolf fourth on C.mid\|Play}}	+7.28
perfect fourth	17	497.56	{{Audio\|17 steps in 41-et on C.mid\|Play}}	4:3	498.04	{{Audio\|Just perfect fourth on C.mid\|Play}}	−0.48
septimal narrow fourth	16	468.29	{{Audio\|16 steps in 41-et on C.mid\|Play}}	21:16	470.78	{{Audio\|Twenty-first harmonic on C.mid\|Play}}	−2.48
septimal major third	15	439.02	{{Audio\|15 steps in 41-et on C.mid\|Play}}	9:7	435.08	{{Audio\|Septimal major third on C.mid\|Play}}	+3.94
undecimal major third	14	409.76	{{Audio\|14 steps in 41-et on C.mid\|Play}}	14:11	417.51	{{Audio\|Undecimal major third on C.mid\|Play}}	−7.75
Pythagorean major third	14	409.76	{{Audio\|14 steps in 41-et on C.mid\|Play}}	81:64	407.82	{{Audio\|Pythagorean_major_third_on_C.mid\|Play}}	+1.94
major third	13	380.49	{{Audio\|13 steps in 41-et on C.mid\|Play}}	5:4	386.31	{{Audio\|Just major third on C.mid\|Play}}	−5.83
tridecimal neutral third, inverted 13th harmonic	12	351.22	{{Audio\|12 steps in 41-et on C.mid\|Play}}	16:13	359.47	{{Audio\|Tridecimal neutral third on C.mid\|Play}}	−8.25
undecimal neutral third	12	351.22	{{Audio\|12 steps in 41-et on C.mid\|Play}}	11:9	347.41	{{Audio\|Undecimal neutral third on C.mid\|Play}}	+3.81
minor third	11	321.95	{{Audio\|11 steps in 41-et on C.mid\|Play}}	6:5	315.64	{{Audio\|Just minor third on C.mid\|Play}}	+6.31
Pythagorean minor third	10	292.68	{{Audio\|10 steps in 41-et on C.mid\|Play}}	32:27	294.13	{{Audio\|Pythagorean_minor_third_in_scale.mid\|Play}}	−1.45
tridecimal minor third	10	292.68	{{Audio\|10 steps in 41-et on C.mid\|Play}}	13:11	289.21	{{Audio\|Tridecimal minor third on C.mid\|Play}}	+3.47
septimal minor third	9	263.41	{{Audio\|9 steps in 41-et on C.mid\|Play}}	7:6	266.87	{{Audio\|Septimal minor third on C.mid\|Play}}	−3.46
septimal whole tone	8	234.15	{{Audio\|8 steps in 41-et on C.mid\|Play}}	8:7	231.17	{{Audio\|Septimal major second on C.mid\|Play}}	+2.97
diminished third	8	234.15	{{Audio\|8 steps in 41-et on C.mid\|Play}}	256:225	223.46	{{Audio\|Just diminished third on C.mid\|Play}}	+10.68
whole tone, major tone	7	204.88	{{Audio\|7 steps in 41-et on C.mid\|Play}}	9:8	203.91	{{Audio\|Major tone on C.mid\|Play}}	+0.97
whole tone, minor tone	6	175.61	{{Audio\|6 steps in 41-et on C.mid\|Play}}	10:9	182.40	{{Audio\|Minor tone on C.mid\|Play}}	−6.79
lesser undecimal neutral second	5	146.34	{{Audio\|5 steps in 41-et on C.mid\|Play}}	12:11	150.64	{{Audio\|Lesser undecimal neutral second on C.mid\|Play}}	−4.30
septimal diatonic semitone	4	117.07	{{Audio\|4 steps in 41-et on C.mid\|Play}}	15:14	119.44	{{Audio\|Septimal diatonic semitone on C.mid\|Play}}	−2.37
Pythagorean chromatic semitone	4	117.07	{{Audio\|4 steps in 41-et on C.mid\|Play}}	2187:2048	113.69	{{Audio\|Pythagorean apotome on C.mid\|Play}}	+3.39
diatonic semitone	4	117.07	{{Audio\|4 steps in 41-et on C.mid\|Play}}	16:15	111.73	{{Audio\|Just diatonic semitone on C.mid\|Play}}	+5.34
Pythagorean diatonic semitone	3	87.80	{{Audio\|3 steps in 41-et on C.mid\|Play}}	256:243	90.22	{{Audio\|Pythagorean_minor_semitone_on_C.mid\|Play}}	−2.42
20:19 wide semitone	3	87.80	{{Audio\|3 steps in 41-et on C.mid\|Play}}	20:19	88.80	{{Audio\|Novendecimal augmented unison on C.mid\|Play}}	−1.00
septimal chromatic semitone	3	87.80	{{Audio\|3 steps in 41-et on C.mid\|Play}}	21:20	84.47	{{Audio\|Septimal chromatic semitone on C.mid\|Play}}	+3.34
chromatic semitone	2	58.54	{{Audio\|2 steps in 41-et on C.mid\|Play}}	25:24	70.67	{{Audio\|Just chromatic semitone on C.mid\|Play}}	−12.14
28:27 wide semitone	2	58.54	{{Audio\|2 steps in 41-et on C.mid\|Play}}	28:27	62.96	{{audio\|Septimal minor second on C.mid\|Play}}	−4.42
septimal comma	1	29.27	{{Audio\|1 step in 41-et on C.mid\|Play}}	64:63	27.26	{{Audio\|Septimal comma on C.mid\|Play}}	+2.00

As the table above shows, the 41-ET both distinguishes between and closely matches all intervals involving the ratios in the harmonic series up to and including the 10th overtone. This includes the distinction between the major tone and minor tone (thus 41-ET is not a meantone tuning). These close fits make 41-ET a good approximation for 5-, 7- and 9-limit music.

41-ET also closely matches a number of other intervals involving higher harmonics. It distinguishes between and closely matches all intervals involving up through the 12th overtones, with the exception of the greater undecimal neutral second (11:10). Although not as accurate, it can be considered a full 15-limit tuning as well.

Tempering

Intervals not tempered out by 41-ET include the diesis (128:125), septimal diesis (49:48), septimal sixth-tone (50:49), septimal comma (64:63), and the syntonic comma (81:80).

41-ET tempers out the 100:99 ratio, which is the difference between the greater undecimal neutral second and the minor tone, as well as the septimal kleisma (225:224), 1029:1024 (the difference between three intervals of 8:7 the interval 3:2), and the small diesis (3125:3072).

References

1. ^"Schismic Temperaments ", Intonation Information.
2. ^"Lattices with Decimal Notation", Intonation Information.
3. ^[https://www.jstor.org/stable/932181] Dirk de Klerk "Equal Temperament", Acta Musicologica, Vol. 51, Fasc. 1 (Jan. - Jun., 1979), pp. 140-150

2 : Equal temperaments|Microtonality

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。