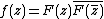“Akhiezer's theorem”的意思、由来-开放百科全书

词条

Akhiezer's theorem

释义

Statement
Related results
Notes
References

In the mathematical field of complex analysis, Akhiezer's theorem is a result about entire functions proved by Naum Akhiezer.^[1]

Statement

Let {{math|f(z)}} be an entire function of exponential type {{math|τ}}, with {{math|f(x) ≥ 0}} for real {{math|x}}. Then the following are equivalent:

There exists an entire function {{math|F}}, of exponential type {{math|τ/2}}, having all its zeros in the (closed) upper half plane, such that

One has:

where {{math|z_n}} are the zeros of {{math|f}}.

Related results

It is not hard to show that the Fejér–Riesz theorem is a special case.^[2]

Notes

1. ^see {{harvtxt|Akhiezer|1948}}.
2. ^see {{harvtxt|Boas|1954}} and {{harvtxt|Boas|1944}} for references.

References

{{ citation

| last = Boas
| first = Jr., Ralph Philip
| title = Entire functions
| publisher = Academic Press Inc.
| location = New York
| year = 1954
| pages = 124–132
}}

{{ citation

| last = Boas
| first = Jr., R. P.
| title = Functions of exponential type. I
| journal = Duke Math. J.
| volume = 11
| year = 1944
| pages = 9–15
| issn = 0012-7094
| doi=10.1215/s0012-7094-44-01102-6
}}

{{citation

| last = Akhiezer
| first = N. I.
| title = On the theory of entire functions of finite degree
| journal = Doklady Akademii Nauk SSSR (N.S.)
| volume = 63
| year = 1948
| pages = 475–478
| mr = 0027333
}}

1 : Theorems in complex analysis

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。