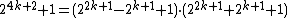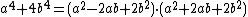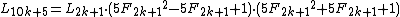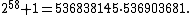- Examples
- History
- References
- External links
In number theory, an aurifeuillean factorization, or aurifeuillian factorization, named after Léon-François-Antoine Aurifeuille, is a special type of algebraic factorization that comes from non-trivial factorizations of cyclotomic polynomials over the integers.[1] Although cyclotomic polynomials themselves are irreducible over the integers, when restricted to particular integer values they may have an algebraic factorization, as in the examples below.
Examples
- Numbers of the form
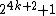have the following aurifeuillean factorization:[2]
- Numbers of the form
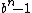or 
, where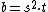 
with square-free 
, have aurifeuillean factorization if and only if one of the following conditions holds:-
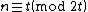
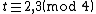and 
-
and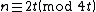 
-
Thus, whenwith square-free
is congruent to
, then if
have aurifeuillean factorization, otherwise,
have aurifeuillean factorization.
When the number is of a particular form (the exact expression varies with the base), Aurifeuillian factorization may be used, which gives a product of two or three numbers. The following equations give Aurifeuillian factors for the Cunningham project bases as a product of F, L and M:[3]
If we let L = C − D, M = C + D, the Aurifeuillian factorizations for bn ± 1 with the bases 2 ≤ b ≤ 24 (perfect powers excluded, since a power of bn is also a power of b) are: (for the coefficients of the polynomials for all square-free bases up to 199 and up to 998, see [4][5])
(Number = F * (C − D) * (C + D) = F * L * M)
| b | Number | (C − D) * (C + D) = L * M | F | C | D |
|---|---|---|---|---|---|
| 2 | 24k + 2 + 1 | 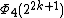 | 1 | 22k + 1 + 1 | 2k + 1 |
| 3 | 36k + 3 + 1 | 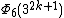 | 32k + 1 + 1 | 32k + 1 + 1 | 3k + 1 |
| 5 | 510k + 5 - 1 | 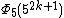 | 52k + 1 - 1 | 54k + 2 + 3(52k + 1) + 1 | 53k + 2 + 5k + 1 |
| 6 | 612k + 6 + 1 | 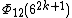 | 64k + 2 + 1 | 64k + 2 + 3(62k + 1) + 1 | 63k + 2 + 6k + 1 |
| 7 | 714k + 7 + 1 | 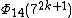 | 72k + 1 + 1 | 76k + 3 + 3(74k + 2) + 3(72k + 1) + 1 | 75k + 3 + 73k + 2 + 7k + 1 |
| 10 | 1020k + 10 + 1 | 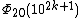 | 104k + 2 + 1 | 108k + 4 + 5(106k + 3) + 7(104k + 2) + 5(102k + 1) + 1 | 107k + 4 + 2(105k + 3) + 2(103k + 2) + 10k + 1 |
| 11 | 1122k + 11 + 1 | 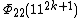 | 112k + 1 + 1 | 1110k + 5 + 5(118k + 4) - 116k + 3 - 114k + 2 + 5(112k + 1) + 1 | 119k + 5 + 117k + 4 - 115k + 3 + 113k + 2 + 11k + 1 |
| 12 | 126k + 3 + 1 | 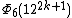 | 122k + 1 + 1 | 122k + 1 + 1 | 6(12k) |
| 13 | 1326k + 13 - 1 | 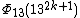 | 132k + 1 - 1 | 1312k + 6 + 7(1310k + 5) + 15(138k + 4) + 19(136k + 3) + 15(134k + 2) + 7(132k + 1) + 1 | 1311k + 6 + 3(139k + 5) + 5(137k + 4) + 5(135k + 3) + 3(133k + 2) + 13k + 1 |
| 14 | 1428k + 14 + 1 | 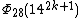 | 144k + 2 + 1 | 1412k + 6 + 7(1410k + 5) + 3(148k + 4) - 7(146k + 3) + 3(144k + 2) + 7(142k + 1) + 1 | 1411k + 6 + 2(149k + 5) - 147k + 4 - 145k + 3 + 2(143k + 2) + 14k + 1 |
| 15 | 1530k + 15 + 1 | 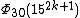 | 1514k + 7 - 1512k + 6 + 1510k + 5 + 154k + 2 - 152k + 1 + 1 | 158k + 4 + 8(156k + 3) + 13(154k + 2) + 8(152k + 1) + 1 | 157k + 4 + 3(155k + 3) + 3(153k + 2) + 15k + 1 |
| 17 | 1734k + 17 - 1 | 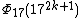 | 172k + 1 - 1 | 1716k + 8 + 9(1714k + 7) + 11(1712k + 6) - 5(1710k + 5) - 15(178k + 4) - 5(176k + 3) + 11(174k + 2) + 9(172k + 1) + 1 | 1715k + 8 + 3(1713k + 7) + 1711k + 6 - 3(179k + 5) - 3(177k + 4) + 175k + 3 + 3(173k + 2) + 17k + 1 |
| 18 | 184k + 2 + 1 | 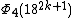 | 1 | 182k + 1 + 1 | 6(18k) |
| 19 | 1938k + 19 + 1 | 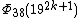 | 192k + 1 + 1 | 1918k + 9 + 9(1916k + 8) + 17(1914k + 7) + 27(1912k + 6) + 31(1910k + 5) + 31(198k + 4) + 27(196k + 3) + 17(194k + 2) + 9(192k + 1) + 1 | 1917k + 9 + 3(1915k + 8) + 5(1913k + 7) + 7(1911k + 6) + 7(199k + 5) + 7(197k + 4) + 5(195k + 3) + 3(193k + 2) + 19k + 1 |
| 20 | 2010k + 5 - 1 | 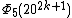 | 202k + 1 - 1 | 204k + 2 + 3(202k + 1) + 1 | 10(203k + 1) + 10(20k) |
| 21 | 2142k + 21 - 1 | 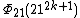 | 2118k + 9 + 2116k + 8 + 2114k + 7 - 214k + 2 - 212k + 1 - 1 | 2112k + 6 + 10(2110k + 5) + 13(218k + 4) + 7(216k + 3) + 13(214k + 2) + 10(212k + 1) + 1 | 2111k + 6 + 3(219k + 5) + 2(217k + 4) + 2(215k + 3) + 3(213k + 2) + 21k + 1 |
| 22 | 2244k + 22 + 1 | 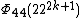 | 224k + 2 + 1 | 2220k + 10 + 11(2218k + 9) + 27(2216k + 8) + 33(2214k + 7) + 21(2212k + 6) + 11(2210k + 5) + 21(228k + 4) + 33(226k + 3) + 27(224k + 2) + 11(222k + 1) + 1 | 2219k + 10 + 4(2217k + 9) + 7(2215k + 8) + 6(2213k + 7) + 3(2211k + 6) + 3(229k + 5) + 6(227k + 4) + 7(225k + 3) + 4(223k + 2) + 22k + 1 |
| 23 | 2346k + 23 + 1 | 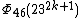 | 232k + 1 + 1 | 2322k + 11 + 11(2320k + 10) + 9(2318k + 9) - 19(2316k + 8) - 15(2314k + 7) + 25(2312k + 6) + 25(2310k + 5) - 15(238k + 4) - 19(236k + 3) + 9(234k + 2) + 11(232k + 1) + 1 | 2321k + 11 + 3(2319k + 10) - 2317k + 9 - 5(2315k + 8) + 2313k + 7 + 7(2311k + 6) + 239k + 5 - 5(237k + 4) - 235k + 3 + 3(233k + 2) + 23k + 1 |
| 24 | 2412k + 6 + 1 | 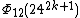 | 244k + 2 + 1 | 244k + 2 + 3(242k + 1) + 1 | 12(243k + 1) + 12(24k) |
(See [6] for more information (square-free bases up to 199))
- Numbers of the form
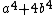have the following aurifeuillean factorization:
- Lucas numbers
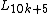have the following aurifeuillean factorization:[7]
whereis the
is the
History
In 1871, Aurifeuille discovered the factorization of 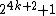for k = 14 as the following:[2][8]
The second factor is prime, and the factorization of the first factor is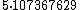 
.[8] The general form of the factorization was later discovered by Lucas.[2]
References
1. ^{{cite journal |url=http://www.ams.org/journals/mcom/2006-75-253/S0025-5718-05-01766-7/S0025-5718-05-01766-7.pdf |title=Aurifeuillian factorization |author=A. Granville, P. Pleasants |journal=Math. Comp. |volume=75 |issue=253 |year=2006 |pages=497–508 |doi=10.1090/S0025-5718-05-01766-7}}
2. ^1 2 {{MathWorld|title=Aurifeuillean Factorization|urlname=AurifeuilleanFactorization}}
3. ^{{cite web|title=Main Cunningham Tables|url=http://homes.cerias.purdue.edu/~ssw/cun/pmain1215|accessdate=21 December 2015|archive-url=https://web.archive.org/web/20160203062607/http://homes.cerias.purdue.edu/~ssw/cun/pmain1215|archive-date=2016-02-03|dead-url=yes|df=}} At the end of tables 2LM, 3+, 5-, 6+, 7+, 10+, 11+ and 12+ are formulae detailing the Aurifeuillian factorisations.
4. ^Coefficients of Lucas C,D polynomials for all square-free bases up to 199
5. ^Coefficients of Lucas C,D polynomials for all square-free bases up to 998
6. ^List of Aurifeuillean factorization
7. ^[https://web.archive.org/web/20081122085141/http://www.utm.edu/research/primes/lists/top20/LucasA.html Lucas Aurifeuilliean primitive part]
8. ^1 Integer Arithmetic, Number Theory – Aurifeuillian Factorizations, Numericana
2. ^1 2 {{MathWorld|title=Aurifeuillean Factorization|urlname=AurifeuilleanFactorization}}
3. ^{{cite web|title=Main Cunningham Tables|url=http://homes.cerias.purdue.edu/~ssw/cun/pmain1215|accessdate=21 December 2015|archive-url=https://web.archive.org/web/20160203062607/http://homes.cerias.purdue.edu/~ssw/cun/pmain1215|archive-date=2016-02-03|dead-url=yes|df=}} At the end of tables 2LM, 3+, 5-, 6+, 7+, 10+, 11+ and 12+ are formulae detailing the Aurifeuillian factorisations.
4. ^Coefficients of Lucas C,D polynomials for all square-free bases up to 199
5. ^Coefficients of Lucas C,D polynomials for all square-free bases up to 998
6. ^List of Aurifeuillean factorization
7. ^[https://web.archive.org/web/20081122085141/http://www.utm.edu/research/primes/lists/top20/LucasA.html Lucas Aurifeuilliean primitive part]
8. ^1 Integer Arithmetic, Number Theory – Aurifeuillian Factorizations, Numericana
External links
- Aurifeuillian Factorisation, Colin Barker
- Online factor collection
1 : Number theory
- Ray Buckland
- Ray Burke (Irish politician)
- Rayburn
- Rayburn House Office Building
- Rayburn range
- Rayburn Township, Armstrong County, Pennsylvania
- Rayburn Township, PA
- Ray Buttigieg
- Ray Cappo
- Ray Carney
- Ray Casey
- Ray Cashley
- Ray casting
- Raycasting
- Ray-casting
- Ray C. Bliss
- Ray C. Ewry
- Ray Chapman
- Ray Charles
- Ray charles
- Ray Charles Live
- Ray Charles Robinson
- Raych Seldon
- Ray City
- Ray (city)