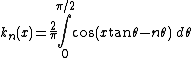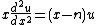- Properties
- References
In mathematics, the Bateman function (or k-function) is a special case of the confluent hypergeometric function studied by Harry Bateman(1931)[1][2]. Bateman defined it by
Bateman discovered this function, when Theodore von Kármán asked for the solution of the following differential equation which appeared in the theory of turbulence[3]
and Bateman found this function as one of the solutions. Bateman denoted this function as "k" function in honor of Theodore von Kármán.
This is not to be confused with another function of the same name which is used in Pharmacokinetics.
Properties
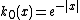
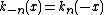
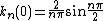
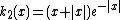
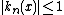 for real values of
for real values of  and
and 
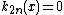 for
for 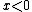 if
if  is a positive integer
is a positive integer- If
 is an odd integer, then
is an odd integer, then 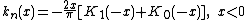 , where
, where  is the Modified Bessel function of the second kind.
is the Modified Bessel function of the second kind.
References
1. ^{{Citation | last1=Bateman | first1=H. | authorlink=Harry Bateman | title=The k-function, a particular case of the confluent hypergeometric function | doi=10.2307/1989510 | mr=1501618 | year=1931 | journal=Transactions of the American Mathematical Society | issn=0002-9947 | volume=33 | issue=4 | pages=817–831}}
2. ^{{Springer|id=B/b015360|title=Bateman function}}
3. ^Martin, P. A., & Bateman, H. (2010). from Manchester to Manuscript Project. Mathematics Today, 46, 82-85. http://www.math.ust.hk/~machiang/papers_folder/http___www.ima.org.uk_mathematics_mt_april10_harry_bateman_from_manchester_to_manuscript_project.pdf
2. ^{{Springer|id=B/b015360|title=Bateman function}}
3. ^Martin, P. A., & Bateman, H. (2010). from Manchester to Manuscript Project. Mathematics Today, 46, 82-85. http://www.math.ust.hk/~machiang/papers_folder/http___www.ima.org.uk_mathematics_mt_april10_harry_bateman_from_manchester_to_manuscript_project.pdf
2 : Special hypergeometric functions|Special functions
- Pro 160C
- Pro 160S
- Pro 24
- Pro-24
- Pro 400H
- Pro7 (Dj/Producer)
- Pro-8
- Pro 800Z
- Pro A
- Proac
- Proacerella
- Proacina
- PROAC (RAF)
- Proacrias
- Proactenis
- Proactica
- Proactinium
- Proactinomyces restrictus
- Proactive cyber defence
- Proactive information delivery
- Proactive learning
- Proactiveness
- Proactive network provider participation for P2P
- Proactive policing
- Proactive secret sharing