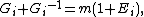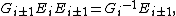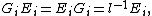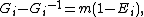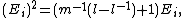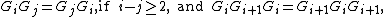“Birman–Wenzl algebra”的意思、由来-开放百科全书

词条

Birman–Wenzl algebra

释义

Definition
Properties
Isomorphism between the BMW algebras and Kauffman's tangle algebras
Baxterisation of Birman-Murakami-Wenzl algebra
History
References

In mathematics, the Birman-Murakami-Wenzl (BMW) algebra, introduced by {{harvtxt|Birman|Wenzl|1989}} and {{harvtxt|Murakami|1986}}, is a two-parameter family of algebras C_n(ℓ, m) of dimension 1·3·5 ··· (2n − 1) having the Hecke algebra of the symmetric group as a quotient. It is related to the Kauffman polynomial of a link. It is a deformation of the Brauer algebra in much the same way that Hecke algebras are deformations of the group algebra of the symmetric group.

Definition

For each natural number n, the BMW algebra C_n(ℓ, m) is generated by G₁,G₂,...,G_n-1,E₁,E₂,...,E_n-1 and relations:

These relations imply the further relations:

This is the original definition given by Birman & Wenzl. However a slight change by the introduction of some minus signs is sometimes made, in accordance with Kauffman's 'Dubrovnik' version of his link invariant. In that way, the fourth relation in Birman & Wenzl's original version is changed to

(1) (Kauffman skein relation)

Given invertibility of m, the rest of the relations in Birman & Wenzl's original version can be reduced to

(2) (Idempotent relation)

(3) (Braid relations)

(4) (Tangle relations)

(5) (Delooping relations)

Properties

The dimension of C_n(ℓ, m) is .
Iwahori-Hecke algebra associated with the symmetric group is a quotient of the Birman-Murakami-Wenzl algebra C_n.
The Braid group embeds in the BMW algebra .

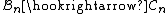Isomorphism between the BMW algebras and Kauffman's tangle algebras

It is proved by {{harvtxt|Morton|Wassermann|1989}} that the BMW algebra C_n(ℓ, m) is isomorphic to the Kauffman's tangle algebra KT_n, the isomorphism is defined by

Baxterisation of Birman-Murakami-Wenzl algebra

Define the face operator as

where and are determined by

and

.

Then the face operator satisfies the Yang-Baxter equation.

Now with

.

In the limits , the braids can be recovered up to a scale factor.

History

In 1984, Vaughan Jones introduced a new polynomial invariant of link isotopy types which is called the Jones polynomial. The invariants are related to the traces of irreducible representations of Hecke algebras associated with the symmetric groups. In 1986, {{harvtxt|Murakami|1986}} showed that the Kauffman polynomial can also be interpreted as a function on a certain associative algebra. In 1989, {{harvtxt|Birman|Wenzl|1989}} constructed a two-parameter family of algebras C_n(ℓ, m) with the Kauffman polynomial K_n(ℓ, m) as trace after appropriate renormalization.

References

{{Citation | doi=10.1090/S0002-9947-1989-0992598-X | last1=Birman | first1=Joan S. | last2=Wenzl | first2=Hans | title=Braids, link polynomials and a new algebra | jstor= 2001074 | mr=992598 | year=1989 | journal=Transactions of the American Mathematical Society | issn=0002-9947 | volume=313 | issue=1 | pages=249–273 | publisher=American Mathematical Society}}
{{Citation | last1=Murakami | first1=Jun | title=The Kauffman polynomial of links and representation theory | url=http://projecteuclid.org/euclid.ojm/1200780357 | mr=927059 | year=1987 | journal=Osaka Journal of Mathematics | issn=0030-6126 | volume=24 | issue=4 | pages=745–758}}
{{cite arxiv | last1=Morton | first1=Hugh R. | last2=Wassermann | first2=A.J.|authorlink2=Antony Wassermann| title=A basis for the Birman-Wenzl algebra | eprint=1012.3116 | year=1989}}

3 : Representation theory|Knot theory|Diagram algebras

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。