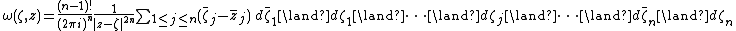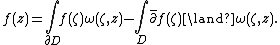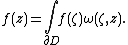请输入您要查询的百科知识：

　

词条 Bochner–Martinelli formula
释义

  1. History

  2. Bochner–Martinelli kernel

  3. See also

  4. Notes

  5. References

In mathematics, the Bochner–Martinelli formula is a generalization of the Cauchy integral formula to functions of several complex variables, introduced by {{harvs|txt|first=Enzo|last=Martinelli| authorlink=Enzo Martinelli|year=1938}} and {{harvs|txt|first=Salomon|last=Bochner|authorlink=Salomon Bochner|year=1943}}.

History

{{quote
|text= Formula (53) of the present paper and a proof of theorem 5 based on it have just been published by Enzo Martinelli (...).[1] The present author may be permitted to state that these results have been presented by him in a Princeton graduate course in Winter 1940/1941 and were subsequently incorporated, in a Princeton doctorate thesis (June 1941) by Donald C. May, entitled: An integral formula for analytic functions of {{math|k}} variables with some applications.
|sign=Salomon Bochner
|source={{harv|Bochner|1943|loc=p. 652, footnote 1}}.
}}{{quote
|text= However this author's claim in loc. cit. footnote 1,[2] that he might have been familiar with the general shape of the formula before Martinelli, was wholly unjustified and is hereby being retracted.
|sign=Salomon Bochner
|source={{harv|Bochner|1947|loc=p. 15, footnote *}}.
}}

Bochner–Martinelli kernel

For {{math|ζ}}, {{math|z}} in ℂn the Bochner–Martinelli kernel {{math|ω(ζ,z)}} is a differential form in {{math|ζ}} of bidegree {{math|(n,n−1)}} defined by

(where the term {{math|d{{overline|ζ}}j}} is omitted).

Suppose that {{math|f}} is a continuously differentiable function on the closure of a domain {{math|D}} in ℂn with piecewise smooth boundary {{math|∂D}}. Then the Bochner–Martinelli formula states that if {{math|z}} is in the domain {{math|D}} then

In particular if {{math|f}} is holomorphic the second term vanishes, so

See also

  • Bergman–Weil formula

Notes

1. ^Bochner refers explicitly to the article {{harv|Martinelli|1942-1943}}, apparently being not aware of the earlier one {{harv|Martinelli|1938}}, which actually contains Martinelli's proof of the formula. However, the earlier article is explicitly cited in the later one, as it can be seen from {{harv|Martinelli|1942-1943|loc=p. 340, footnote 2}}.
2. ^Bochner refers to his claim in {{harv|Bochner|1943|loc=p. 652, footnote 1}}.

References

{{refbegin}}
  • {{Citation

|last = Aizenberg
|first = L. A.
|author-link = Lev Aizenberg
|last2 = Yuzhakov
|first2 = A. P.
|author2-link = Aleksandr Yuzhakov
|title = Integral Representations and Residues in Multidimensional Complex Analysis
|url = https://books.google.com/books?id=2ZWsf6ufee8C&printsec=frontcover&hl=en&#v=onepage&q&f=true
|place = Providence R.I.
|series = Translations of Mathematical Monographs
|volume = 58
|publisher = American Mathematical Society
|pages = x+283
|year = 1983
|origyear = 1979
|isbn = 0-8218-4511-X
|mr = 0735793
|zbl = 0537.32002

}}.

  • {{Citation

|last1=Bochner
|first1=Salomon
|author1-link=Salomon Bochner
|title=Analytic and meromorphic continuation by means of Green's formula
|jstor=1969103
|mr=0009206
|zbl = 0060.24206
|series=Second Series
|year=1943
|journal=Annals of Mathematics
|issn=0003-486X
|doi=10.2307/1969103
|volume=44
|pages=652–673
|subscription=yes}}.
  • {{Citation

|last1 = Bochner
|first1 = Salomon
|author1-link = Salomon Bochner
|title = On compact complex manifolds
|journal = The Journal of the Indian Mathematical Society
|series = New Series,
|volume = 11
|pages = 1–21
|year = 1947
|url =
|doi =
|mr = 0023919
|zbl = 0038.23701

}}.

  • {{eom|id=b/b016720|first=E.M.|last= Chirka|title=Bochner–Martinelli representation formula}}
  • {{Citation

|last=Krantz
|first=Steven G.
|author-link= Steven G. Krantz
|title=Function theory of several complex variables
|url=https://books.google.com/books?isbn=9780821827246
|publisher=AMS Chelsea Publishing
|year=2001
|origyear=1992
|edition=reprint of 2nd
|pages = xvi+564
|place= Providence, R.I.
|isbn=978-0-8218-2724-6
|mr=1846625
|zbl=1087.32001
|doi=10.1090/chel/340

}}.

  • {{Citation

|last = Kytmanov
|first = Alexander M.
|author-link = Alexander Kytmanov
|title=The Bochner-Martinelli integral and its applications
|origyear = 1992
|url=https://books.google.com/books?isbn=376435240X
|publisher = Birkhäuser Verlag
|pages = xii+305
|year = 1995
|isbn = 978-3-7643-5240-0
|mr = 1409816
|zbl = 0834.32001
|doi=10.1007/978-3-0348-9094-6

}}.

  • {{Citation

|last = Kytmanov
|first = Alexander M.
|author-link = Alexander Kytmanov
|last2 = Myslivets
|first2 = Simona G.
|author2-link =
|title = Интегральные представления и их приложения в многомерном комплексном анализе
|trans-title = Integral representations and their application in multidimensional complex analysis
|url = http://www.eastview.com/russian/books/product.asp?SKU=930345B&f_locale=_CYR&active_tab=1
|place = Красноярск
|publisher = СФУ
|pages = 389
|year = 2010
|isbn = 978-5-7638-1990-8
|mr =
|zbl =
|deadurl = yes
|archiveurl = https://web.archive.org/web/20140323020317/http://www.eastview.com/russian/books/product.asp?SKU=930345B&f_locale=_CYR&active_tab=1
|archivedate = 2014-03-23
|df =

}}.

  • {{Citation

|last = Kytmanov
|first = Alexander M.
|author-link = Alexander Kytmanov
|last2 = Myslivets
|first2 = Simona G.
|author2-link =
|title = Multidimensional integral representations. Problems of analytic continuation
|url = https://books.google.com/books?id=jpWKCgAAQBAJ&printsec=frontcover&hl=it#v=onepage&q&f=true
|place = Cham–Heidelberg–New York–Dordrecht–London
|publisher = Springer Verlag
|pages = xiii+225
|year = 2015
|isbn = 978-3-319-21658-4
|doi=10.1007/978-3-319-21659-1
|mr = 3381727
|zbl = 1341.32001

}}, {{ISBN|978-3-319-21659-1}} (ebook).

  • {{Citation

|last=Martinelli
|first=Enzo
|author-link=
|title=Alcuni teoremi integrali per le funzioni analitiche di più variabili complesse
|trans-title=Some integral theorems for analytic functions of several complex variables
|language = Italian
|year=1938
|journal=Atti della Reale Accademia d'Italia. Memorie della Classe di Scienze Fisiche, Matematiche e Naturali
|issue=7
|volume=9
|pages=269–283
|id=
|jfm= 64.0322.04
|zbl = 0022.24002

}}. The first paper where the now called Bochner-Martinelli formula is introduced and proved.

  • {{Citation

|last = Martinelli
|first = Enzo
|author-link =
|title = Sopra una dimostrazione di R. Fueter per un teorema di Hartogs
|trans-title = On a proof of R. Fueter of a theorem of Hartogs
|language = Italian
|journal = Commentarii Mathematici Helvetici
|volume = 15
|issue = 1
|pages = 340–349
|year = 1942–1943
|url = http://retro.seals.ch/digbib/en/view?rid=comahe-002:1942-1943:15::26
|doi = 10.5169/seals-14896
|mr = 0010729
|zbl = 0028.15201
|deadurl = yes
|archiveurl = https://web.archive.org/web/20111002072948/http://retro.seals.ch/digbib/en/view?rid=comahe-002%3A1942-1943%3A15%3A%3A26
|archivedate = 2011-10-02
|df =

}}. Available at the SEALS Portal. In this paper Martinelli gives a proof of Hartogs' extension theorem by using the Bochner-Martinelli formula.

  • {{Citation

|last = Martinelli
|first = Enzo
|author-link =
|title = Introduzione elementare alla teoria delle funzioni di variabili complesse con particolare riguardo alle rappresentazioni integrali
|trans-title=Elementary introduction to the theory of functions of complex variables with particular regard to integral representations
|language = Italian
|place = Rome
|publisher = Accademia Nazionale dei Lincei
|year = 1984
|series = Contributi del Centro Linceo Interdisciplinare di Scienze Matematiche e Loro Applicazioni
|volume = 67
|pages = 236+II
|url = http://www.lincei.it/pubblicazioni/catalogo/volume.php?lg=e&rid=33233
|doi =
|id =
|isbn =

}}. The notes form a course, published by the Accademia Nazionale dei Lincei, held by Martinelli during his stay at the Accademia as "Professore Linceo".

  • {{Citation

|last = Martinelli
|first = Enzo
|title = Qualche riflessione sulla rappresentazione integrale di massima dimensione per le funzioni di più variabili complesse
|trans-title=Some reflections on the integral representation of maximal dimension for functions of several complex variables
|language = Italian
|journal = Atti della Accademia Nazionale dei Lincei. Rendiconti. Classe di Scienze Fisiche, Matematiche e Naturali
|series = Series VIII
|url=http://www.bdim.eu/item?fmt=pdf&id=RLIN_1984_8_76_4_235_0
|volume = 76
|issue = 4
|pages = 235–242
|year = 1984b
|mr=0863486
|zbl = 0599.32002

}}. In this article, Martinelli gives another form to the Martinelli–Bochner formula.

{{refend}}{{DEFAULTSORT:Bochner-Martinelli formula}}

2 : Theorems in complex analysis|Several complex variables
随便看

　

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。

　

Copyright © 2023 OENC.NET All Rights Reserved
京ICP备2021023879号 更新时间：2024/11/11 5:56:36