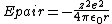- Derivation Electrostatic potential Repulsive term Total energy
- Calculated lattice energies
- Born Exponent
- See also
- References
The Born–Landé equation is a means of calculating the lattice energy of a crystalline ionic compound. In 1918[1] Max Born and Alfred Landé proposed that the lattice energy could be derived from the electrostatic potential of the ionic lattice and a repulsive potential energy term.[2]
where:
- NA = Avogadro constant;
- M = Madelung constant, relating to the geometry of the crystal;
- z+ = numeric charge number of cation
- z− = numeric charge number of anion
- e = elementary charge, 1.6022{{e|−19}} C
- ε0 = permittivity of free space
4πε0 = 1.112{{e|−10}} C2/(J·m)
- r0 = distance to closest ion
- n = Born exponent, typically a number between 5 and 12, determined experimentally by measuring the compressibility of the solid, or derived theoretically.[3]
Derivation
The ionic lattice is modeled as an assembly of hard elastic spheres which are compressed together by the mutual attraction of the electrostatic charges on the ions. They achieve the observed equilibrium distance apart due to a balancing short range repulsion.
Electrostatic potential
The electrostatic potential energy, Epair, between a pair of ions of equal and opposite charge is:
where
z = magnitude of charge on one ion
e = elementary charge, 1.6022{{e|−19}} C
ε0 = permittivity of free space
4{{pi}}ε0 = 1.112{{e|−10}} C2/(J·m)
r = distance separating the ion centers
For a simple lattice consisting ions with equal and opposite charge in a 1:1 ratio, interactions between one ion and all other lattice ions need to be summed to calculate EM, sometimes called the Madelung or lattice energy:
where
M = Madelung constant, which is related to the geometry of the crystal
r = closest distance between two ions of opposite charge
Repulsive term
Born and Lande suggested that a repulsive interaction between the lattice ions would be proportional to {{sfrac|1|r{{isup|n}}}} so that the repulsive energy term, ER, would be expressed:
where
B = constant scaling the strength of the repulsive interaction
r = closest distance between two ions of opposite charge
n = Born exponent, a number between 5 and 12 expressing the steepness of the repulsive barrier
Total energy
The total intensive potential energy of an ion in the lattice can therefore be expressed as the sum of the Madelung and repulsive potentials:
Minimizing this energy with respect to r yields the equilibrium separation r0 in terms of the unknown constant B:
Evaluating the minimum intensive potential energy and substituting the expression for B in terms of r0 yields the Born–Landé equation:
Calculated lattice energies
The Born–Landé equation gives a reasonable fit to the lattice energy.[2]
| Compound | Calculated | Experimental |
|---|---|---|
| NaCl | −756 kJ/mol | −787 kJ/mol |
| LiF | −1007 kJ/mol | −1046 kJ/mol |
| CaCl2 | −2170 kJ/mol | −2255 kJ/mol |
Born Exponent
The Born exponent is typically between 5 and 12. Approximate experimental values are listed below:[4]
| Ion configuration | He | Ne | Ar, Cu+ | Kr, Ag+ | Xe, Au+ |
|---|---|---|---|---|---|
| n | 5 | 7 | 9 | 10 | 12 |
See also
- Kapustinskii equation
- Born–Mayer equation
References
2. ^1 {{cite book|title=Metals and chemical change|year=2002|publisher=Royal Society of Chemistry|location=Cambridge|isbn=0-85404-665-8|last=Johnson|first=the Open University ; RSC ; edited by David|edition=1. publ.}}
3. ^{{Cotton&Wilkinson4th}}
4. ^{{cite web|url=http://alpha.chem.umb.edu/chemistry/ch370/CH370_Lectures/Lecture%20Documents/Ch07_2_LatticeEnergy.pdf|title=Lattice Energy}}
- Herochroma mansfiedi
- Herochroma ochreipicta
- Herochroma orientalis
- Herochroma pallensia
- Herochroma perspicillata
- Herochroma rosulata
- Herochroma sinapiaria
- Herochroma supraviridaria
- Herochroma viridaria
- Herochroma yazakii
- Hero cities
- Hero city
- Hero class cutter
- Hero-class patrol vessel
- Heroclitus
- Hero.com
- Hero comic book
- H. E. R. O. (comics)
- H E R O (comics)
- Hero comics
- HERO (comics)
- Hero complex
- Hero Con
- Herocore
- Hero Core