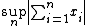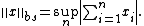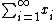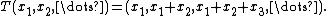“Bs space”的意思、由来-开放百科全书

词条

Bs space

释义

In the mathematical field of functional analysis, the space bs consists of all infinite sequences (x_i) of real or complex numbers such that

is finite. The set of such sequences forms a normed space with the vector space operations defined componentwise, and the norm given by

Furthermore, with respect to metric induced by this norm, bs is complete: it is a Banach space.

The space of all sequences (x_i) such that the series

is convergent (possibly conditionally) is denoted by cs. This is a closed vector subspace of bs, and so is also a Banach space with the same norm.

The space bs is isometrically isomorphic to the space of bounded sequences ℓ^∞ via the mapping

Furthermore, the space of convergent sequences c is the image of cs under T.

References

{{citation|first1=N.|last1=Dunford|first2=J.T.|last2=Schwartz|title=Linear operators, Part I|publisher=Wiley-Interscience|year=1958}}.

2 : Banach spaces|Functional analysis

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。