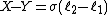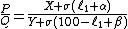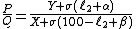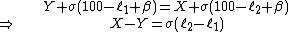“Carey Foster bridge”的意思、由来-开放百科全书

词条

Carey Foster bridge

释义

Use
To measure σ
Theory
References

In electronics, the Carey Foster bridge is a bridge circuit used to measure medium resistances, or to measure small differences between two large resistances. It was invented by Carey Foster as a variant on the Wheatstone bridge. He first described it in his 1872 paper "On a Modified Form of Wheatstone's Bridge, and Methods of Measuring Small Resistances" (Telegraph Engineer's Journal, 1872–1873, 1, 196).

Use

In the adjacent diagram, X and Y are resistances to be compared. P and Q are nearly equal resistances, forming the other half of the bridge. The bridge wire EF has a jockey contact D placed along it and is slid until the galvanometer G measures zero. The thick-bordered areas are thick copper busbars of almost zero resistance.

Place a known resistance in position Y.
Place the unknown resistance in position X.
Adjust the contact D along the bridge wire EF so as to null the galvanometer. This position (as a percentage of distance from E to F) is {{math|ℓ₁}}.
Swap X and Y. Adjust D to the new null point. This position is {{math|ℓ₂}}.
If the resistance of the wire per percentage is {{math|σ}}, then the resistance difference is the resistance of the length of bridge wire between {{math|ℓ₁}} and {{math|ℓ₂}}:

To measure a low unknown resistance X, replace Y with a copper busbar that can be assumed to be of zero resistance.

In practical use, when the bridge is unbalanced, the galvanometer is shunted with a low resistance to avoid burning it out. It is only used at full sensitivity when the anticipated

measurement is close to the null point.

To measure σ

To measure the unit resistance of the bridge wire EF, put a known resistance (e.g., a standard 1 ohm resistance) that is less than that of the wire as X, and a copper busbar of assumed zero resistance as Y.

Theory

Two resistances to be compared, X and Y, are connected in series with the bridge wire. Thus, considered as a Wheatstone bridge, the two resistances are X plus a length of bridge wire, and Y plus the remaining bridge wire. The two remaining arms are the nearly equal resistances P and Q, connected in the inner gaps of the bridge.

Let {{math|ℓ₁}} be the null point D on the bridge wire EF in percent. {{math|α}} is the unknown left-side extra resistance EX and {{math|β}} is the unknown right-side extra resistance FY, and {{math|σ}} is the resistance per percent length of the bridge wire:

and add 1 to each side:

(equation 1)

Now swap X and Y. {{math|ℓ₂}} is the new null point reading in percent:

and add 1 to each side:

(equation 2)

Equations 1 and 2 have the same left-hand side and the same numerator on the right-hand side, meaning the denominator on the right-hand side must also be equal:

Thus: the difference between X and Y is the resistance of the bridge wire between {{math|ℓ₁}} and {{math|ℓ₂}}.

The bridge is most sensitive when P, Q, X and Y are all of comparable magnitude.

References

Carey Foster Bridge (PDF) (St.Stephen's College, Delhi University){{dead link|date=November 2015}}
{{cite journal

| title = Obituary notices: .... George Carey Foster, 1835–1919; .....
| pages = 412–427
| author = A. H. Fison
| doi = 10.1039/CT9191500408
| journal = J. Chem. Soc., Trans.
| volume = 115
| issue =
| year = 1919}}{{Bridge circuits}}

5 : Analog circuits|Measuring instruments|Bridge circuits|English inventions|Impedance measurements

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。