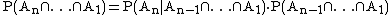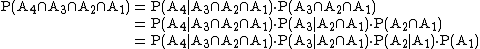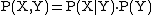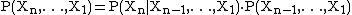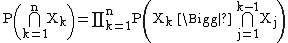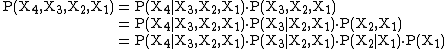“Chain rule (probability)”的意思、由来-开放百科全书

词条

Chain rule (probability)

释义

Chain rule for events
Two events Example More than two events Example
Chain rule for random variables
Two random variables More than two random variables Example
Footnotes
References

In probability theory, the chain rule (also called the general product rule{{sfn|Schum|1994}}{{sfn|Klugh|2013}}) permits the calculation of any member of the joint distribution of a set of random variables using only conditional probabilities. The rule is useful in the study of Bayesian networks, which describe a probability distribution in terms of conditional probabilities.

Chain rule for events

Two events

The chain rule for two random events and says

.

Example

This rule is illustrated in the following example. Urn 1 has 1 black ball and 2 white balls and Urn 2 has 1 black ball and 3 white balls. Suppose we pick an urn at random and then select a ball from that urn. Let event be choosing the first urn: 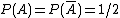. Let event be the chance we choose a white ball. The chance of choosing a white ball, given that we have chosen the first urn, is 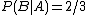. Event 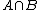would be their intersection: choosing the first urn and a white ball from it. The probability can be found by the chain rule for probability:

.

More than two events

For more than two events the chain rule extends to the formula

which by induction may be turned into

.

Example

With four events (), the chain rule is

Chain rule for random variables

Two random variables

For two random variables , to find the joint distribution, we can apply the definition of conditional probability to obtain:

More than two random variables

Consider an indexed collection of random variables 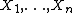. To find the value of this member of the joint distribution, we can apply the definition of conditional probability to obtain:

Repeating this process with each final term creates the product:

Example

With four variables (), the chain rule produces this product of conditional probabilities:

Footnotes

References

{{cite book|first=David A.|last=Schum|title=The Evidential Foundations of Probabilistic Reasoning|year=1994|publisher=Northwestern University Press|isbn=978-0-8101-1821-8|page=49|ref=harv}}
{{cite book|first=Henry E.|last=Klugh|title=Statistics: The Essentials for Research|year=2013|publisher=Psychology Press|isbn=1-134-92862-9|page=149|edition=3rd|ref=harv}}
{{Russell Norvig 2003}}, p. 496.
[https://www.ibm.com/developerworks/mydeveloperworks/blogs/nlp/entry/the_chain_rule_of_probability "The Chain Rule of Probability"], developerWorks, Nov 3, 2012.

3 : Probability theory|Bayesian inference|Bayesian statistics

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。