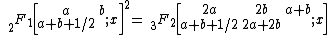“Clausen's formula”的意思、由来-开放百科全书

词条

Clausen's formula

释义

References

In mathematics, Clausen's formula, found by {{harvs |txt |authorlink=Thomas Clausen (mathematician) |first=Thomas |last=Clausen |year=1828}}, expresses the square of a Gaussian hypergeometric series as a generalized hypergeometric series. It states

In particular it gives conditions for a hypergeometric series to be positive. This can be used to prove

several inequalities, such as the Askey–Gasper inequality used in the proof of de Branges's theorem.

References

{{Citation | last1=Andrews | first1=George E. | last2=Askey | first2=Richard | last3=Roy | first3=Ranjan | title=Special functions | publisher=Cambridge University Press | series=Encyclopedia of Mathematics and its Applications | isbn=978-0-521-62321-6 | mr=1688958 | year=1999 | volume=71}}
{{Citation | last1=Clausen | first1=Thomas | title= Ueber die Fälle, wenn die Reihe von der Form y = 1 + ... etc. ein Quadrat von der Form z = 1 ... etc.hat | url=http://www.digizeitschriften.de/main/dms/toc/?PPN=PPN243919689_0003 | year=1828 | journal= Journal für die reine und angewandte Mathematik | volume=3 }}
For a detailed proof of Clausen's formula: {{Citation | last1=Milla | first1=Lorenz | title= A detailed proof of the Chudnovsky formula with means of basic complex analysis | arxiv=1809.00533 | year=2018 }}

1 : Special functions

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。