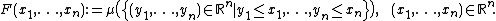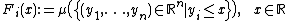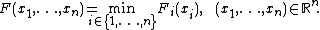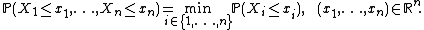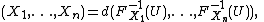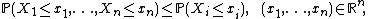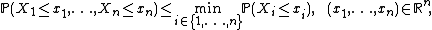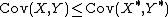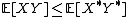“Comonotonicity”的意思、由来-开放百科全书

词条

Comonotonicity

释义

Definitions
Comonotonicity of subsets of {{math|Rⁿ}} Comonotonicity of probability measures on {{math|Rⁿ}} Comonotonicity of {{math|Rⁿ}}-valued random vectors
Properties
Upper bounds
Upper Fréchet–Hoeffding bound for cumulative distribution functions Upper bound for the covariance
See also
Notes
Citations
References

In probability theory, comonotonicity mainly refers to the perfect positive dependence between the components of a random vector, essentially saying that they can be represented as increasing functions of a single random variable. In two dimensions it is also possible to consider perfect negative dependence, which is called countermonotonicity.

Comonotonicity is also related to the comonotonic additivity of the Choquet integral.^[1]

The concept of comonotonicity has applications in financial risk management and actuarial science, see e.g. {{harvtxt|Dhaene|Denuit|Goovaerts|Vyncke|2002a}} and {{harvtxt|Dhaene|Denuit|Goovaerts|Vyncke|2002b}}. In particular, the sum of the components {{math|X₁ + X₂ + · · · + X_n}} is the riskiest if the joint probability distribution of the random vector {{math|(X₁, X₂, . . . , X_n)}} is comonotonic.^[2] Furthermore, the {{math|α}}-quantile of the sum equals of the sum of the {{math|α}}-quantiles of its components, hence comonotonic random variables are quantile-additive.^[3]^[4] In practical risk management terms it means that there is minimal (or eventually no) variance reduction from diversification.

For extensions of comonotonicity, see {{harvtxt|Jouini|Napp|2004}} and {{harvtxt|Puccetti|Scarsini|2010}}.

Definitions

Comonotonicity of subsets of {{math|Rⁿ}}

A subset {{math|S}} of {{math|Rⁿ}} is called comonotonic^[5] (sometimes also nondecreasing^[6]) if, for all {{math|(x₁, x₂, . . . , x_n)}} and {{math|(y₁, y₂, . . . , y_n)}} in {{math|S}} with {{math|x_i < y_i}} for some {{math|i ∈ {1, 2, . . . , n}}}, it follows that {{math|x_j ≤ y_j}} for all {{math|j ∈ {1, 2, . . . , n}}}.

This means that {{math|S}} is a totally ordered set.

Comonotonicity of probability measures on {{math|Rⁿ}}

Let {{math|μ}} be a probability measure on the {{math|n}}-dimensional Euclidean space {{math|Rⁿ}} and let {{math|F}} denote its multivariate cumulative distribution function, that is

Furthermore, let {{math|F₁, . . . , F_n}} denote the cumulative distribution functions of the {{math|n}} one-dimensional marginal distributions of {{math|μ}}, that means

for every {{math|i ∈ {1, 2, . . . , n}}}. Then {{math|μ}} is called comonotonic, if

Note that the probability measure {{math|μ}} is comonotonic if and only if its support {{math|S}} is comonotonic according to the above definition.^[7]

Comonotonicity of {{math|Rⁿ}}-valued random vectors

An {{math|Rⁿ}}-valued random vector {{math|X {{=}} (X₁, . . . , X_n)}} is called comonotonic, if its multivariate distribution (the pushforward measure) is comonotonic, this means

Properties

An {{math|Rⁿ}}-valued random vector {{math|X {{=}} (X₁, . . . , X_n)}} is comonotonic if and only if it can be represented as

where {{math|{{=}}_d}} stands for equality in distribution, on the right-hand side are the left-continuous generalized inverses^[8] of the cumulative distribution functions {{math|F_X₁, . . . , F_{X_n}}}, and {{math|U}} is a uniformly distributed random variable on the unit interval. More generally, a random vector is comonotonic if and only if it agrees in distribution with a random vector where all components are non-decreasing functions (or all are non-increasing functions) of the same random variable.^[9]

Upper bounds

Upper Fréchet–Hoeffding bound for cumulative distribution functions

Let {{math|X {{=}} (X₁, . . . , X_n)}} be an {{math|Rⁿ}}-valued random vector. Then, for every {{math|i ∈ {1, 2, . . . , n}}},

hence

with equality everywhere if and only if {{math|(X₁, . . . , X_n)}} is comonotonic.

Upper bound for the covariance

Let {{math|(X, Y)}} be a bivariate random vector such that the expected values of {{math|X}}, {{math|Y}} and the product {{math|XY}} exist. Let {{math|(X^*, Y^*)}} be a comonotonic bivariate random vector with the same one-dimensional marginal distributions as {{math|(X, Y)}}.^[10] Then it follows from Höffding's formula for the covariance^[11] and the upper Fréchet–Hoeffding bound that

and, correspondingly,

with equality if and only if {{math|(X, Y)}} is comonotonic.^[12]

Note that this result generalizes the rearrangement inequality and Chebyshev's sum inequality.

Notes

1. ^{{harv|Sriboonchitta|Wong|Dhompongsa|Nguyen|2010|pp=149–152}}
2. ^{{harv|Kaas|Dhaene|Vyncke|Goovaerts|2002|loc=Theorem 6}}
3. ^{{harv|Kaas|Dhaene|Vyncke|Goovaerts|2002|loc=Theorem 7}}
4. ^{{harv|McNeil|Frey|Embrechts|2005|loc=Proposition 6.15}}
5. ^{{harv|Kaas|Dhaene|Vyncke|Goovaerts|2002|loc=Definition 1}}
6. ^See {{harv|Nelsen|2006|loc=Definition 2.5.1}} for the case {{math|n {{=}} 2}}
7. ^See {{harv|Nelsen|2006|loc=Theorem 2.5.4}} for the case {{math|n {{=}} 2}}
8. ^{{harv|McNeil|Frey|Embrechts|2005|loc=Proposition A.3 (properties of the generalized inverse)}}
9. ^{{harv|McNeil|Frey|Embrechts|2005|loc=Proposition 5.16 and its proof}}
10. ^{{math|(X^*, Y^*)}} always exists, take for example {{math|(F_X⁻¹(U), F_Y⁻¹(U))}}, see section Properties above.
11. ^{{harv|McNeil|Frey|Embrechts|2005|loc=Lemma 5.24}}
12. ^{{harv|McNeil|Frey|Embrechts|2005|loc=Theorem 5.25(2)}}

Citations

References

{{Citation

| last1 = Dhaene
| first1 = Jan
| last2 = Denuit
| first2 = Michel
| last3 = Goovaerts
| first3 = Marc J.
| last4 = Vyncke
| first4 = David
| title = The concept of comonotonicity in actuarial science and finance: theory
| journal = Insurance: Mathematics & Economics
| volume = 31
| issue = 1
| pages = 3–33
| year = 2002a
| url = http://www.econ.kuleuven.be/insurance/pdfs/DdgkvTh.pdf
| mr = 1956509
| zbl = 1051.62107
| doi=10.1016/s0167-6687(02)00134-8}}

{{Citation

{{Citation

| last = Jouini
| first = Elyès
| last2 = Napp
| first2 = Clotilde
| title = Conditional comonotonicity
| journal = Decisions in Economics and Finance
| volume = 27
| issue = 2
| pages = 153–166
| year = 2004
| issn = 1593-8883
| url = http://www.ceremade.dauphine.fr/~jouini/DEF180RR.pdf
| mr = 2104639
| zbl = 1063.60002
| doi=10.1007/s10203-004-0049-y}}

{{Citation

| last = Kaas
| first = Rob
| last2 = Dhaene
| first2 = Jan
| last3 = Vyncke
| first3 = David
| last4 = Goovaerts
| first4 = Marc J.
| last5 = Denuit
| first5 = Michel
| title = A simple geometric proof that comonotonic risks have the convex-largest sum
| journal = ASTIN Bulletin
| volume = 32
| issue = 1
| pages = 71–80
| year = 2002
| url = http://www.casact.org/library/astin/vol32no1/71.pdf
| mr = 1928014
| zbl = 1061.62511
| doi=10.2143/ast.32.1.1015}}

{{Citation

| last = McNeil
| first = Alexander J.
| last2 = Frey
| first2 = Rüdiger
| last3 = Embrechts
| first3 = Paul
| title = Quantitative Risk Management. Concepts, Techniques and Tools
| place = Princeton, NJ
| publisher = Princeton University Press
| series = Princeton Series in Finance
| year = 2005
| url = https://books.google.com/books?id=f5J_OZPeq50C
| isbn = 978-0-691-12255-7
| mr = 2175089
| zbl = 1089.91037}}

{{Citation

{{Citation

| last = Puccetti
| first = Giovanni
| last2 = Scarsini
| first2 = Marco
| title = Multivariate comonotonicity
| journal = Journal of Multivariate Analysis
| volume = 101
| issue = 1
| pages = 291–304
| year = 2010
| url = http://www.parisschoolofeconomics.eu/IMG/pdf/MED090320-Scarsini.pdf
| issn = 0047-259X
| mr = 2557634
| zbl = 1184.62081
| doi=10.1016/j.jmva.2009.08.003}}

{{Citation

| last = Sriboonchitta
| first = Songsak
| last2 = Wong
| first2 = Wing-Keung
| last3 = Dhompongsa
| first3 =Sompong
| last4 = Nguyen
| first4 = Hung T.
| title = Stochastic Dominance and Applications to Finance, Risk and Economics
| place = Boca Raton, FL
| publisher = Chapman & Hall/CRC Press
| year = 2010
| url = https://books.google.com/books?id=omxatN4lVCkC
| isbn = 978-1-4200-8266-1
| mr = 2590381
| zbl = 1180.91010}}

3 : Theory of probability distributions|Independence (probability theory)|Covariance and correlation

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。