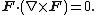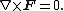- See also
- Notes
- References
In vector calculus, a complex lamellar vector field is a vector field in three dimensions which is orthogonal to its own curl. That is,
Complex lamellar vector fields are precisely those that are normal to a family of surfaces. A special case are irrotational vector fields, satisfying
An irrotational vector field is locally the gradient of a function, and is therefore orthogonal to the family of level surfaces (the equipotential surfaces). Accordingly, the term lamellar vector field is sometimes used as a synonym for an irrotational vector field.[1]
The adjective "lamellar" derives from the noun "lamella", which means a thin layer. The lamellae to which "lamellar flow" refers are the surfaces of constant potential, or in the complex case, the surfaces orthogonal to the vector field.
See also
- Beltrami vector field
- Conservative vector field
Notes
References
- {{citation | title=Vectors, tensors, and the basic equations of fluid mechanics | first=Rutherford | last=Aris | authorlink=Rutherford Aris| publisher=Dover | year=1989 | isbn=0-486-66110-5 }}
- Millerhof
- Miller Homes
- Miller Homestead
- Miller Homestead (Au Sable, New York)
- Miller Homestead (Pea Ridge, Arkansas)
- Miller Hook
- Miller House (Columbus, Indiana)
- Miller House (disambiguation)
- Miller / Hull
- Miller/Hull Partnership
- Milleria
- Millerian
- Miller Ice Rise
- Millerieae
- Miller, Indiana
- Miller indice
- Miller Institute
- Miller Institute for Basic Research in Science
- Miller Institute knot
- Miller Island
- Millerites
- Mille River
- Miller, John Jackson
- Miller, Kansas
- Miller-Kingsland House